In the previous blog, we talked briefly about tabular Q-learning, however this method can be prone to noises within reward realisations. In this blog, we briefly cover two extensions to Q-learning, and how these ideas can be further extended in a more complex setting.
One way we can hedge against overestimation bias caused by noise is to use a method known as double Q-learning. This method is analogous to tabular Q-learning, with the extension being having two tables to store Q values instead of one.
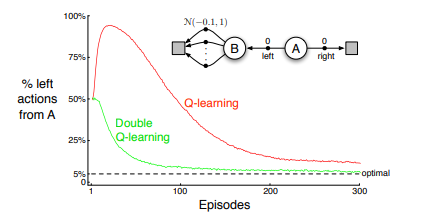
The difference between this and tabular Q-learning other than having two tables to store Q values is within the update function, where we randomly update one Q function using the “optimal” future action which is derived from the other Q table. This can be defined by,
Q_1(s,a) \leftarrow Q_1(s,a) + \alpha \left[R(s,a) + \gamma Q_1\left(s', \arg\max_{a'} Q_2(s',a')\right) - Q_1(s,a) \right], Q_2(s,a) \leftarrow Q_2(s,a) + \alpha \left[R(s,a) + \gamma Q_2\left(s', \arg\max_{a'} Q_1(s',a')\right) - Q_2(s,a) \right].This method has been shown to have the same computational time as tabular Q-learning, but requires double the memory. Hence, this method struggles even further in scalability. However, the idea has been fundamental when applied to further extensions of Q-learning which aimed to deal with large state and/or action space.
References:
Sutton, R. S. and Barto, A. G. (2018). Reinforcement Learning: An Introduction. MIT Press, 2nd edition.
Van Hasselt, H. (2010). Double Q-learning. Advances in neural information processing systems, 23.