Tower of Hanoi – Lídia André

I remember my parents taking my brother and I to Pavilhão do Conhecimento, a science museum in Lisbon, to spend a day there at least once a year when we were little. And I remember that I loved those days. There were a lot of things we could do there, from playing “grown-ups” to solving “little” mathematical problems (and here I say little because they were easy enough for a kid to solve without getting frustrated). One of the problems available for us to solve was the Tower of Hanoi consisting of only 3 discs. In this post I will talk briefly about this problem and why it may be hard to solve.

Problem

The Tower of Hanoi problem consists of 3 rods and $n$ discs of different sizes. Roughly, the goal of the problem is to move the stack of discs from the leftmost rod to the rightmost rod. However, as all problems, some rules have to be followed:

We can only move one disc at a time
We can also only move a disc if it is the uppermost disc on a stack
Finally, we cannot place a larger disc on top of a smaller one. In other words, we will always need to have cone-shape towers

So, the simple example I had in my visits to Pavilhão do Conhecimento can be solved as shown in the figure below:

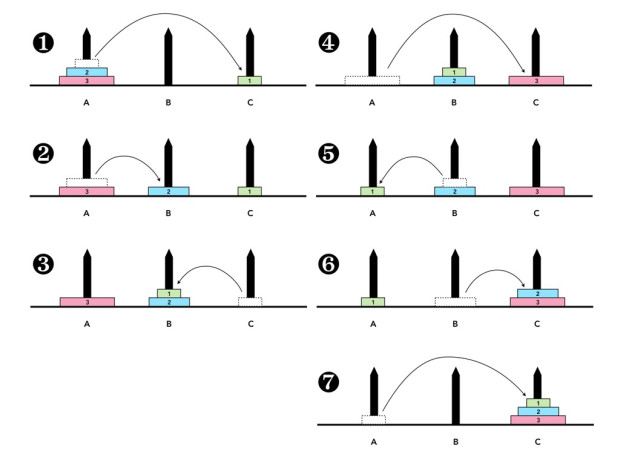
We can see that $7$ steps were required to solve this simple example. This corresponds to $2^n-1$ . You can start to see why this may be difficult to solve in some situations. Imagine if you had $10$ discs, you would solve the problem in $1023$ steps. You may argue it’s doable but you would need a lot of patience to spend time moving pieces $1023$ times.

So, what can be done to efficiently determine the steps to take with a fairly large number of discs? Well, we can construct an algorithm. If we think about it, we can solve the Tower of Hanoi problem for $n$ discs by solving it for $n-1$ discs. And we can solve the problem with $n-1$ discs by solving it for $n-2$ disks. And you get the idea: each smaller stack is a sub-problem of the original. For this motive, we can solve the problem by using a recursive algorithm. So, to move $n$ discs from the leftmost rod, say $A$ , to the rightmost rod, say $C$ , the algorithm can be

Move $n-1$ discs from $A$ to $B$ (steps 1 to 3 on the image)
Move the last, and larger, disc from $A$ to $C$ (step 4 on the image)
Move $n-1$ discs from $B$ to $C$ (steps 5 to 7 on the image)

Note that step 1 can be solved taking the exact three steps, and so on.

Conclusion

It may seem a simple enough problem to solve but, in reality, as the complexity of the algorithm is proportional to $2^n$ , it will take a long time to solve when the number of discs is large.

I hope you found this post interesting! If so, you can read more about the Tower of Hanoi problem here:

See you on my next post!

S	M	T	W	T	F	S
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30	31