The title of my PhD is “Stochastic Programming Approaches to the Storage Location Assignment Problem”. The problem is application driven, aiming to create models for optimising how products are placed and picked in large, industrial-sized warehouses. My project is specifically researching how stochastic programming can be used to this end, with consideration of randomness from unknown orders arriving at the warehouse. My project is a joint collaboration between Lancaster University’s STOR-i CDT and Tesco. My academic supervisors are Dr Jamie Fairbrother and Dr Luke Rhodes-Leader, and my industrial supervisors are Dr Edwin Reynolds, Dr Ben Black, Dr Fotios Katsigiannis and Dr Thomas Wilson.
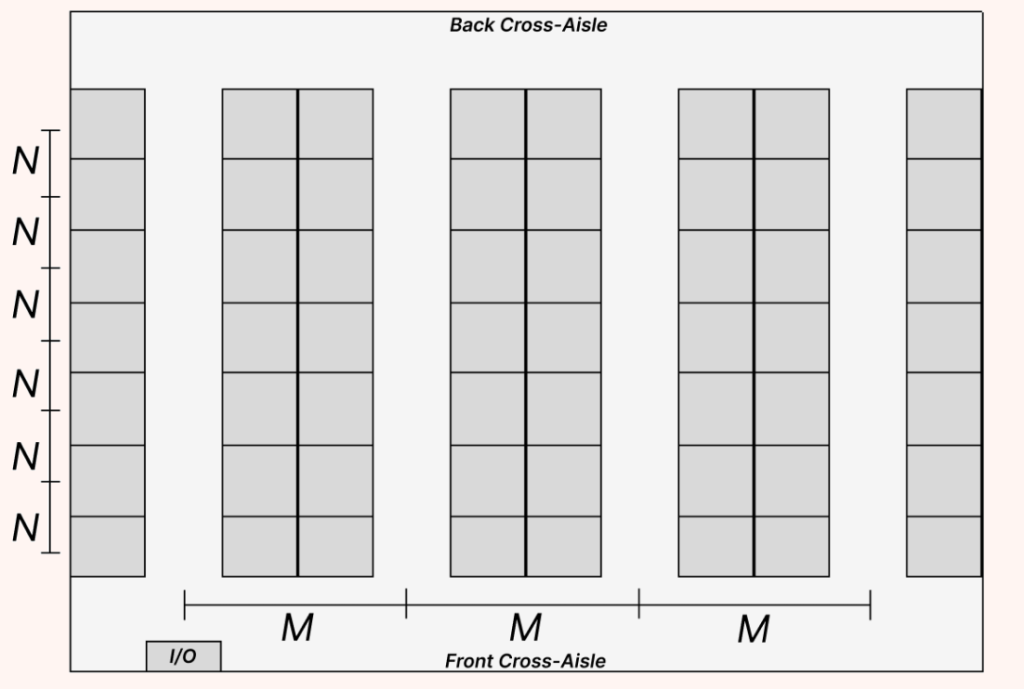
In the problem we are considering, we have a single-block warehouse like that shown above. The warehouse is divided into parallel aisles, each of which are split into bays. We have a front cross-aisle and a back cross-aisle, and pickers (staff responsible for picking products from shelves) are permitted to travel bidirectionally through the aisles and cross-aisles. This layout is the most widely-studied of warehouse layouts, and is reminiscent of many warehouses used in practice by retail companies.
The aim of the problem is to minimise the distance travelled by pickers, and it can naturally be broken down into three distinct stages.
- Storage Assignment: Products are assigned to slots in the warehouse, where each slot is represented by an (aisle, bay) pair
- Order Batching: Orders are batched together before they are picked
- Picker Routing: Routes are selected for pickers to take when collecting orders
These stages can be solved in a sequential or an integrated framework. In true operations there is a place for both – for full warehouse reshuffles, for example once per season, all stock can be moved and an integrated approach taken. For daily orders, only the batching and routing needs to be solved. Naturally, techniques developed for the former can easily be extended to the latter.

During my PhD, I will be using stochastic programming approaches to construct optimisation models aimed at solving the SLAP in an integrated way. A key priority will be in improving scalability. This can be done in three distinct ways: firstly, modelling techniques can be used to create tight formulations with small technology matrices and few variables, particularly auxiliary variables. This, used in conjunction with tailored solution algorithms, can be applied broadly to all new models. To complement this, the second approach is to reduce the size of the problem by leveraging problem-specific operational constraints, such as one-way systems and the clustering of products based on slot capacities. Thirdly, input reduction techniques can be used to reduce the size of problems through the careful selection of a small subset of orders which well-approximate the global set whilst reducing the requirement of the model to optimise over large inputs. Using these, we aim to scale stochastic programmes which accurately model the problem to warehouses of a size which is of genuine interest and use to industry.
