II Classical computation
II.1 von Neumann architecture
Computers store and process information. All common computers feature a combination of input and output devices, memory, processing unit, and control unit, which is known as the von Neumann architecture. This architecture is designed to store and process information flexibly by means of programs, which encode a sequence of instructions. These features also apply to the proposed quantum computers. The difference between both types of devices consists in how they represent and manipulate the information. In this section, we describe how this works for classical computers.
II.2 Binary representation of information
Classical computers represent information digitally as binary numbers , where the binary digits (or bits) can take values or 1, and can be presented as a sequence (sometimes, leading zeros are dropped). For example, the binary number is identical to the decimal number 3, and the binary number is identical to the decimal number 34. These numbers can be interpreted in many different ways — they may represent a letter (as in the ASCII code), or the color or brightness of a pixel on a computer monitor. They therefore represent various types of information.
II.3 Quantifying classical information
From a physical perspective, the transmission of large amounts of binary data results in an irregular sequence of discrete events which is best described in the language of statistical mechanics. This provides means to precisely quantify the information content of the data, as well as its degradation due to imperfections in transmission and manipulation processes.
Consider a register with binary digits (bits). This can represent different numbers. When we add a register with bits, this increases to (where ). However, since physically we simply added components, the data capacity of the composed register is far more conveniently specified by describing it as an -bit register. The desired additive measure of storage capacity is therefore , , where is the logarithm with base 2 (such that ). This is nothing else but the entropy
of a system with microstates, which are all occupied with equal probability . The entropy defined here is known as the Shannon entropy, and differs from the entropy in thermodynamics only by a multiplicative factor (where is Boltzmann’s constant).
The entropy is a convenient measure of information content particularly when one considers that we usually do not make best use of the register states. E.g., the ASCII code only has 7 bits (the 8th bit in a byte can therefore be used to check for errors, i.e., it adds redundancy). Morẹovẹr, in tẹxts wẹ only usẹ printablẹ charactẹrs, and somẹ charactẹrs (such as ẹ) occur far morẹ frẹquẹntly than othẹrs (such as q). The different register states then no longer occur with equal probability , which is exploited by compression algorithms (frequent symbols—or combinations of symbols—are abbreviated by short bit sequences). The entropy tells us to how many bits a data stream can be ideal compressed—this is Shannon’s noiseless channel coding theorem.
The entropy can also be used to quantify the degradation of the information content due to transmission errors. Assuming that bits are flipped randomly with error rate , the capacity of a channel reduces by a factor . Another source of errors are lost data packages—this is especially prevalent in wireless transmission and satellite communication.
Errors can be detected and corrected by adding additional bits—naively, by repeatedly sending the same data stream; more effectively, by adding other means of redundancy, such as using the 8th bit in the ASCII code for a parity check. Fortunately, Shannon’s noisy channel coding theorem ensures the existence of error-correction codes which make the error probability arbitrarily small (see section VI.1 for examples of error-correction schemes).
II.4 Operations
Consider a memory unit which contains bits. Such a unit is also called a register. The specified register can represent binary numbers, which range from to . In order to carry out computations, we need facilities to transform any of these numbers into any other number in the same range. It turns our that this is possible with a sequence of operations which act either only on one bit (called unary operations), or on a pair of bits (called binary operations). Furthermore, because bits only take two possible values, these operations can be formulated using the concepts of Boolean logic, the mathematical discipline of TRUE and FALSE statements, which are conventionally associated with the values 1 and 0, respectively.
Each type of logical operation is called a gate. Graphically, a gate is represented by a box, with horizontal lines to the left representing input channels and horizontal lines to the right representing output channels (see Fig. 1). The operation of the gate is specified by a truth table, which specifies the output values as function of the input values. Below, for compactness, we express these outputs as simple algebraic functions of the inputs.
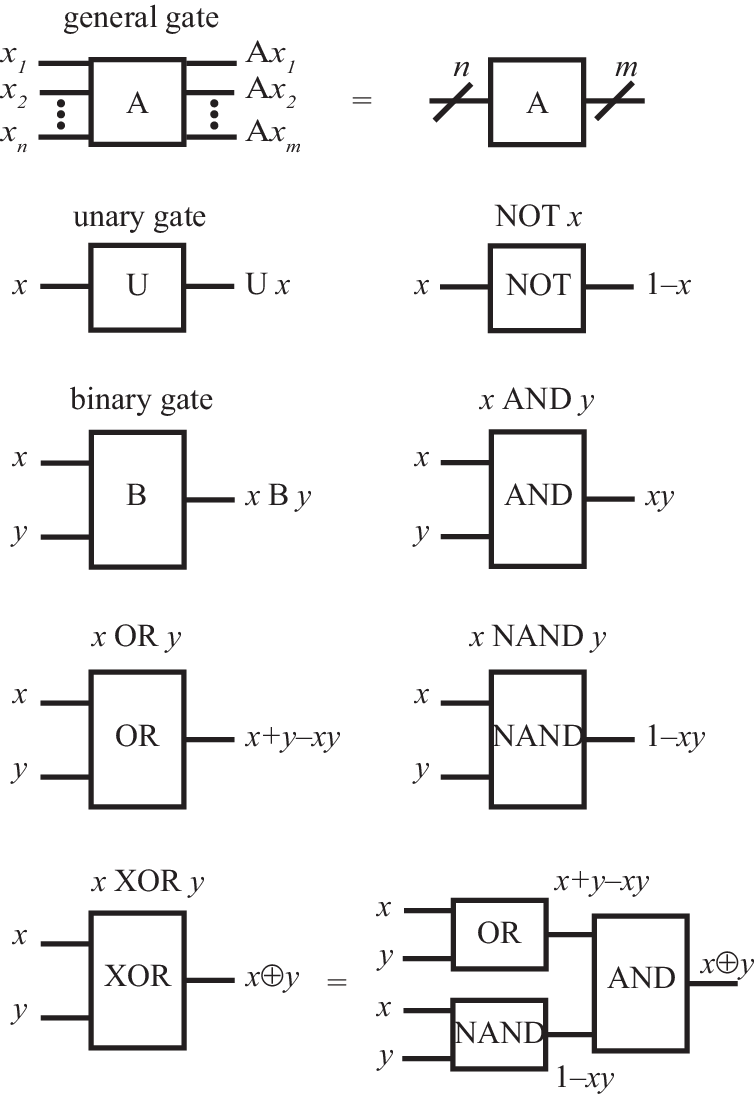
II.5 Unary and binary gates
There are four unary gates (i.e., gates that take one bit as input): The identity gate which lets the bit intact, the not gate which inverts (or flips) the value of the bit, and the two reset gates , , for which the output is independent of the input.
There are 16 binary gates (gates that take two bits as input), of which the following ones are particularly noteworthy: The and gate , which outputs TRUE only if both and are TRUE, the or gate , which outputs TRUE if at least one of and are TRUE, the exclusive-or gate (where denotes addition modulo 2), and the negated-and gate . These gates are not independent; for example, we can write
Indeed, it is possible to write all unary and binary operations only using the NAND gate (e.g., ). Together with the capability to replicate (or copy) information, this is sufficient to achieve all possible operations.
II.6 Reversible gates
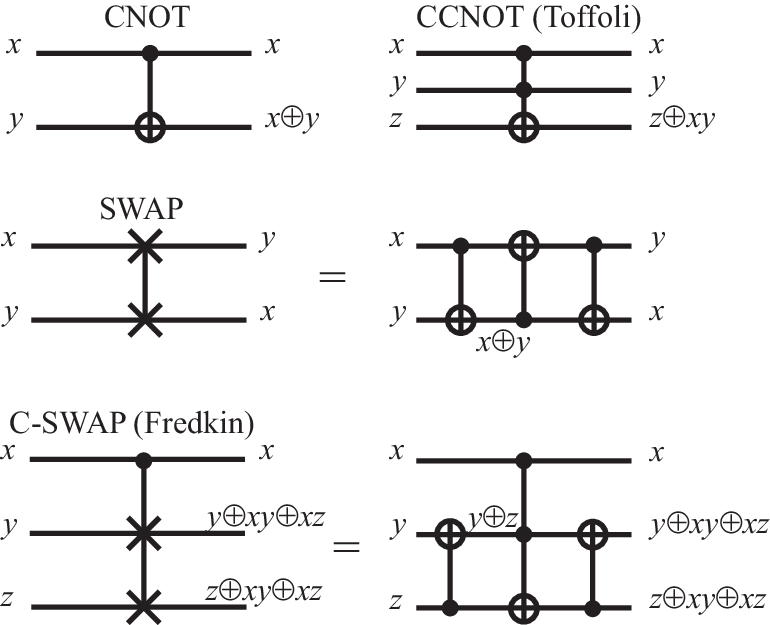
With exception of Id and NOT, the gates discussed so far are irreversible: knowing only the output, it is impossible to infer the input. It is noteworthy that one can also implement classical computations with a set of reversible gates, which have additional output channels that allow to infer the input values (see Fig. 2). The most important example is the controlled-not gate , which flips the target bit if the control bit is TRUE, and otherwise leaves the target bit unchanged (the first bit therefore controls whether the second bit is flipped or not). Because , this gate can be used to copy information. Another example is the SWAP gate , which interchanges the values of the two bits. As indicated in Fig. 2, this can be implemented by combining three CNOT gates. The figure also shows two important reversible three-bit gate, the Toffoli gate (also known as CCNOT gate), which transforms , and the Fredkin gate (also known as controlled swap), which transforms and . A universal set of reversible gates needs to include at least one of these three-bit gates.
II.7 Complexity of computational tasks
We will later see that quantum computers can achieve certain tasks in a relatively small number of operations. In order to gauge their efficiency, it is useful to distinguish computational tasks by their complexity. Let us assume we want to operate on registers with bits, and denote the number of operations required for specific a task (such as the multiplication of two numbers with bits) by . If grows as a polynomial with , the task is relatively simple; this pertains, e.g., to arithmetic and algebraic tasks, such as matrix inversion. Problems of this kind are grouped into complexity class . Many problems, however, are much harder, and require a number of operations which grows exponentially with . A notable example is the factorization of large numbers into prime factors, for which no algorithm in is known. For this specific problem it is, however, easy to verify that the solution (once found) is correct — this simply requires multiplication of the factors, which is a task in . Such problems are called nondeterministic polynomial, and grouped in class NP. Interestingly, there are problems to which all other NP problems can be reduced; such problems are called NP-complete, and a large number of them is known. What is not known is the answer to the fundamental question whether the complexity classes and NP actually differ — one cannot exclude that there is an undiscovered algorithm which solves an NP-complete problem in a polynomial number of operations. If such an algorithm would be identified, it could be used to solve all NP problems much more efficiently than presently possible.
II.8 Practical issues
In order to build a workable computer, the theoretical concepts presented here must be complemented by practical considerations. Available computers preferably use irreversible logics based on gates which dissipate energy, not least because this provides a much larger degree of stability than reversible gates. For efficiency, they use more than a minimally required set of gates, which reduces the number of necessary operations. Furthermore, they use many different methods to physically represent the bits, e.g., by means of different voltages in components of the electronic circuit in the processing unit, or by different magnetization of domains in hard-disk storage units. Over the years, the feature size of electronic circuits has shrunken steadily, which slowly but surely brings them close to the threshold where they become susceptible to quantum effects. As we will see in the next sections (III-V), these effects are not necessarily unwelcome, as they can be exploited to achieve tasks that are hard to achieve with classical computers, which leads to the concept of a quantum computer. However, quantum computation is far more error prone than classical computation, which brings about a new range of practical issues that are discussed in section VI.2.