The Time Window Assignment Vehicle Routing Problem
Transportation plays a vital role across social and economic activities today and is a key contributor to the UK economy. As a result, planning the best routes for delivery vehicles is very important. However, this is not easy as there are many restrictions to consider, such as traffic, time limits, fuel use and customer locations. The Vehicle Routing Problem (VRP) is a well-studied combinatorial optimisation problem addressing this challenge.
In many contexts, such as deliveries from warehouses to shops, deliveries are made on a regular basis, and a time window must be assigned to each shop well in advance, even though the demand is unknown and may vary. Delivery schedules must follow the set time window for each shop. The Time Window Assignment Vehicle Routing Problem (TWAVRP) is a variant of the VRP addressing this situation. Since the time window allocation must occur before demand is known, this is a two-stage stochastic problem. The TWAVRP is a strongly NP hard problem. My project aims to develop methods for solving the TWAVRP, with current focus on the deterministic equivalent framework.
Report: The Capacitated Vehicle Routing Problem
As part of the MRes at STOR-i, students are asked to complete a technical research report into an area of interest. The topic I selected was the Capacitated Vehicle Routing Problem (CVRP), where I focused on the wide range of formulations for the CVRP, and investigated the relative strengths of these formulations. This project laid a strong foundation for what would later become my PhD research, which looks at a variant of the CVRP which incorporates time windows.
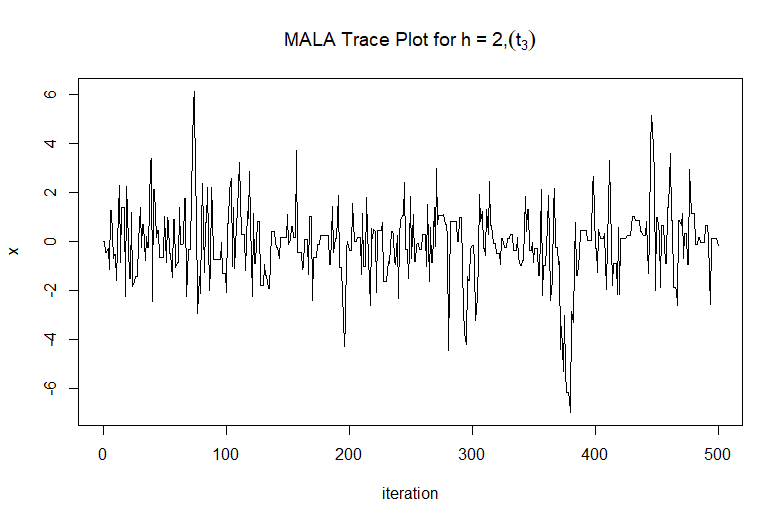
Report: MCMC algorithms: a comparison of exact and approximate methods
As a part of my MRes at STOR-i, I completed a research report focused on Markov chain Monte Carlo. In this report, I focus on comparing exact and approximate methods for MCMC, including the random walk Metropolis, MALA, ULA and SGLA.
Masters dissertation: The Mathieu groups
In the final year of my undergraduate degree, I completed my Master’s dissertation, focusing on constructing the large Mathieu groups, M22, M23, and M24. In this dissertation, my approach for the construction of the Mathieu groups concerns one-point extensions of the projective geometry PG(2,4).