In my previous post, I talked about the statistics research project that I did as part of the STOR-i program. Today I will discuss the Operational Research project I worked on with Kevin Glazebrook about Optimal Patrolling.
Consider an art gallery with several rooms. Some of these rooms are connected directly by doorways but for some pairs of rooms it may be necessary to pass through one or more intermediary rooms in order to travel between them. Each room in the gallery contains various valuable pieces of artwork. At night, when the gallery is closed, a single guard must patrol the area to prevent thievery or vandalism from instituters (attackers). The Patrol Problem is to find a patrol route that minimizes the expected cost of any damage caused by attackers.
To approach this problem we must first create a model and make some modelling assumptions.
We can use the ideas from my post on The seven bridges of Königsberg to represent the rooms of the gallery as nodes on a graph as shown in the example below:
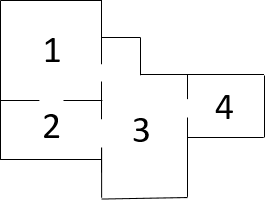
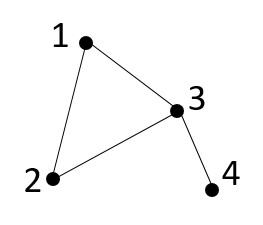
We assume that the total value of the artwork in each room is known to both the patroller and any potential attacker. We also assume that the length of time taken to carry out an attack in any given room is random but is sampled from a known distribution.
Our patrol model assumes that the attackers arrive according to a Poisson process with a known rate and then decide which room to attack in one of the two follow ways:
- The target of the attack is chosen at random with known probabilities.
- The target of each attack is chosen strategically with the presence of a patroller in mind and the aim to maximize the total expected cost of the attacks.
The patroller is assumed to move between rooms in discrete time-steps. If the patroller interrupts an attack in progress, we assume that no damage is caused.
We need a way to tell the patroller which is the best route to take.
If the attackers choose where to attack using the randomised method we have the following:
While visiting a location the patroller either determines that no attacks are underway or apprehends the attacker. Thus, we know that immediately after a visit to a location, no attackers are present. It therefore makes sense to characterize the system by a vector containing the number of time-steps since patroller visited each room. We call this the state of the model.
If we assume that the time it takes to carry out an attack has some maximum, we can ensure the number of states is finite. This is because once we have neglected a room long enough, increasing the time since the last visit will not change the probability that an attack is ongoing.
The current room can be determined from the state as it will correspond to the entry with the lowest value. A patrol policy then tells the patroller what to do in any given state: either stay where you are or move to an adjacent room.
Since there are a finite number or states and a finite number of rooms we have a finite number of policies. An optimal policy can be found using linear programming.
If the attackers choose where to attack strategically we can create a two-person zero sum game as discussed by in my post on game theory.
In either case the optimal solution is very computationally expensive to calculate and so approximate methods are often preferred.
