Recent Comments
STOR-i conference poster
Posted in Uncategorised
1 Comment
A multi-modal distribution.
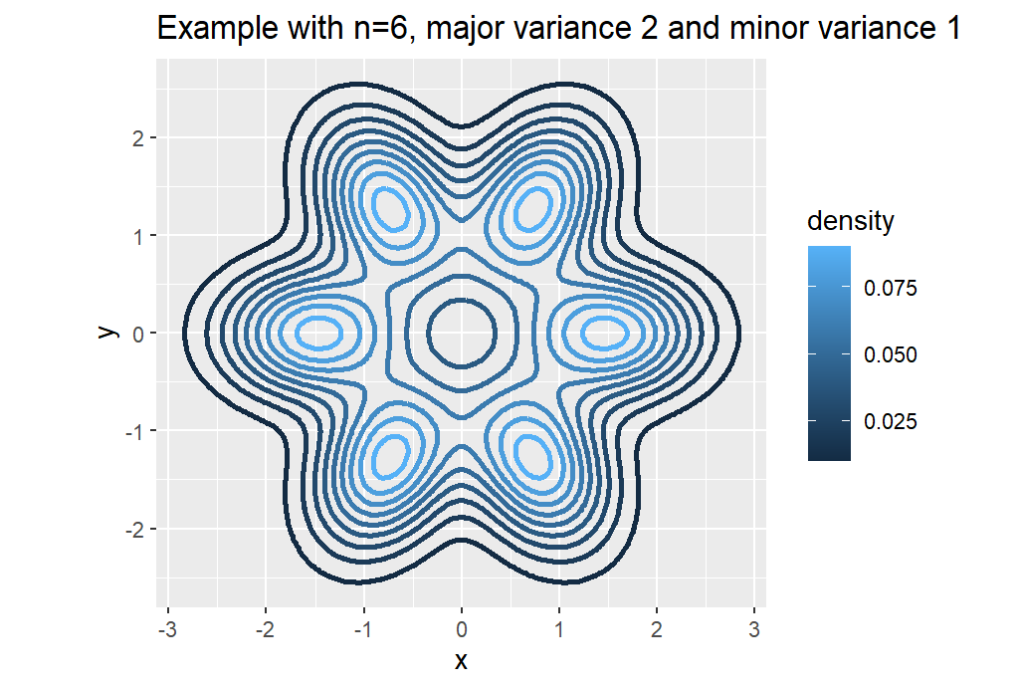
I created a simple bivariate distribution which I will describe in this post. This is a toy example of a multi-modal distribution which I used to test different MCMC methods including parallel tempering and HMC for one of the first reports I wrote for the MRes.
The distribution is a mixture of bivariate normal distributions, with means at the vertices of a regular polygon in the plane.
That is for some n-gon, we place our modes \mu_k the vertices are at the points
\mu_k = R ( \cos \left( \frac{2\pi k}{n}\right), \sin\left( \frac{2\pi k}{n}\right))^t, \ \text{ for } k = 1,2,\ldots, n.The mixture target distribution is a weighted sum of multivariate normal distributions,
\pi(x) = \sum_{k=1}^n w_k N(\mu_k,\Sigma_k).The weights are such that \sum_{k=1}^n w_k =1. For example, one can take w_k = \frac{1}{n}. Now I would like each of the covariance matrices to be oriented such that the principal eigenvector points towards the origin. We can achieve this by means of a change of basis,
\Sigma_k = \begin{pmatrix}\cos \left( \frac{2\pi k}{n}\right) & -\sin \left( \frac{2\pi k}{n}\right) \\ \sin \left( \frac{2\pi k}{n}\right) & \cos \left( \frac{2\pi k}{n}\right)\end{pmatrix}\begin{pmatrix} \sigma_1^2 & 0 \\ 0 & \sigma_2^2 \end{pmatrix}\begin{pmatrix}\cos \left( \frac{2\pi k}{n}\right) & -\sin \left( \frac{2\pi k}{n}\right) \\ \sin \left( \frac{2\pi k}{n}\right) & \cos \left( \frac{2\pi k}{n}\right)\end{pmatrix}^{-1}.Here’s an example: