STOR-i Conference 2016
10th January 2016
In the last few days I have attended the two day annual
STOR-i Conference. This brought together STOR-i students and STOR-i partners (both industrial and academic) to share and discuss
their recent work and progress, ranging from applications of OR in quantative finance and windfarm placement to space time modelling
of infectious diseases. There were a mixture of talks, posters and an opportunity to interact with the speakers. It was very
enjoyable with some really interesting presentations. The purpose of this post is to share some of the topics, ideas and methods raised
during the conference.

The first topic I want to discuss was brought up by the very first speaker, Pitu Mirchandani, from the School of Computing,
Informatics, and Decision Systems Engineering at Arizona State University. He fired up the conference by discussing issues raised by
the limited distance electric vehicles (EV) can travel on one battery. Limted range and limited charging/battery exchange (BE) points means that finding the
shortest drive between origin and destination is not just a matter of finding the shortest route. Careful planning is required in order
to make sure one can even make the journey, never mind make it quickly. Unless there exist sufficient refuelling stations along the
unconstrained best route, there are bound to be detours.
Suppose that we have a network, \(G\), of \(n\) nodes and \(m\) arcs (connections between two nodes). Let $R$ be the subset of nodes
that are BE points. We are aiming to get from the start, $s$, to the destination , $t$. If the shortest path is greater than our
limited range, $c$, we must stop along the way. Therefore, the problem becomes a matter of solving the shortest path problem multiple times
(from $s$ to a BE node, to another BE node, ... to $t$). As the shortest path wouldn't result in us refuelling at the same BE twice,
the shortest path problem is solved at most $(|R|+1)$ times. Therefore, it can be solved in polynomial time
\(\left(\mathcal{O}\left(|R|(\log_2n+m)\right)\right)\).
Following this, the talk went on to describe another problem regarding the location of refuelling points. What is the optimal positioning
of refuelling points in order to minimise the detours required? The current case being studied is that of a tree (see diagram) with $n$ nodes.
If we wish to add at least $p$ BE points to the network, there must be at least
one BE within $c$ of each node. This is straightforward to solve if there are just two nodes, or even three with one junction. However,
as more and more nodes are added, the complexity increases vastly, the problem is NP hard. This will be the future work of Mirchandani
in the year to come.

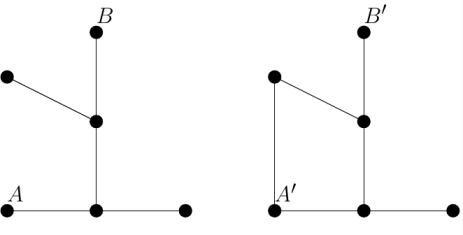
The graph on the left is a tree (notice you can only get from $A$ to $B$ in one way). The graph on the right is not a tree as there
are two possible routes from $A'$ to $B'$.
The next topic I would like to talk about was raised by Steve Scott from Google. His talk explained how multi-arm bandits can be
used when experimenting with multiple versions of the same website. Multi-armed bandit problem comes from how to choose which slot
machine to use in order to get the most money back. The experiment is done by directing different interent users to different versions
of the website. Suppose that the probabilty of getting reward $y$ from version $a$ is $f_a(y|\theta)$. Clearly, we want to choose $a$
to maximse the reward. However, we don't know what $\theta$ is, so how can we make that decision?
His solution is to consider it within the context of Bayesian statistics. Using a prior distribution $p(\theta)$ and data
$\mathbf{y}$, one can obtain the posterior distribution as $$p(\theta|y) \propto p(\theta)f_a(y|\theta).$$ Next, Scott used a heuristic
known as Thompson sampling. We randomly allocate units (in our context, users) to each slot machine in proportion to the probability that that
machine is the best. How do we work this out though?

Well, first we simulate $N$ samples, $\theta^{(1)},...,\theta^{(N)}$, from the posterior. Next we compute the reward of action $a$
given $\theta$, $v_a(\theta)$, for each sample. If $I_a(\theta)$ is 1 if action $a$ gives the largest reward for a given $\theta$
and 0 otherwise, we estimate the probability of machine $a$ being the best by $$w_a=\frac{1}{N}\sum_{g=1}^NI_a\left(\theta^{(g)}\right),$$
that is, the fraction of the sample $\theta^{(1)},...,\theta^{(N)}$ for which action $a$ gives the best reward.
Scott showed us the results of some "experiments" for which one website was slightly better than another. The Thompson sampling enabled
him to distinguish which was better (up to 95% confidence) using less data (and therefore time) than other methods. As this uses less
time, less reward is lost by the experimenter, and so the cost of the experiment is reduced.
I hope this short report has been of interest. For a brief explanation of some of the other things that went on at the STOR-i conference
and more details about Mirchandani's work, have a look at the references.
References
[1] STOR-i Conference Abstracts
[2] New Logistical Issues in Using Electric Vehicle Fleets with Battery Exchange Infrastructure, P. Mirchandani,
J. Adler, O. Madsen, Procedia - Social and Behavioural Sciences, Vol.108, pp.3-14 (2014)