In this two part series of blog posts, we will explore how a simple game of seemingly random choice, inspired by an innocuous 60’s TV show can result in an intriguing investigation into both the simplicity and deceitful nature of probability.
Pick a door, any door
In a 1975 letter to the American Statistician, Steve Selvin posed a problem loosely based off the 1960’s American TV show Let’s Make a Deal. The game consisted of three doors, two of which had goats behind them, and a third door containing a dream car. The host of the show, Monty Hall, asks the contestant to select a door. Monty then chooses a remaining door to reveal a goat. He then asks the contestant if they would like to switch to the one remaining unrevealed door, or stay with their initial choice.
Years later in 1990, Marilyn vos Savant, who rose to fame for her supposedly record high IQ, was posed a similar question in her “Ask Marilyn” column for Parade magazine (which is still running today!). The responses of both Selvin and vos Savant respectively, postulated that it will be in the best interest for
the contestant to switch doors.
This came as a rather counterintuitive conclusion to many as it may be initially thought that there is no difference in staying or switching, there is a still a 50% chance the car lies behind either remaining door. This idea was widely shared amongst the public, with Vos Savant receiving 10,000 complaints for her statistical heresy. How could it be a better option to switch doors? The criticism ranged from soccer moms, to amateur Mathematicians, and even those possessing PhD’s in Maths based disciplines.

However the two savvy protagonists of this story were correct in their rational… and more importantly, had the maths to prove it.
The host knows all
To understand why it is in our best interest to switch, let’s pose the problem in a more formal sense by having a run through. We have three doors that can be labelled 1,2,3. Our esteemed host, Monty Hall, asks the contestant to pick a door. Say they pick door 1. Monty, who knows what’s behind each door, opens door 2 and reveals a goat. He then poses the question ”would you like to stick with your choice or switch to door three?”. To help quell the contestants dilemma, we can first think about the odds of initially picking the correct door. With three doors, the contestant has a 1/3 chance of picking correct straight away. Then if we remove a door, does that change our odds when switching?

One naive way to think about it is that, if each door has equal probability, surely switching makes no difference? Since removing a door will leave us with two options, we must have a 1/2 chance of winning either way? The problem with this approach is we do not account for the host knowing what is behind each door. Given that the first door possesses a probability of 1/3 of containing our Car. The other two doors must attain a 2/3 probability it lies behind either one; and behind one of these doors, must lie a
goat. Since Monty knows that, in this scenario, door 2 has a goat, this door is revealed and we are left with the option of switching to door 3. Yet we still have a 2/3 probability that the Car doesn’t lie behind the first door, so this probability carries over to represent just door 3. Hence we have probabilities of 1/ 3 for door 1, 0 for door 2, and 2/3 for door 3. Concluding that switching will be the correct decision to this dilemma.
Our newest contestant, Thomas Bayes
Wordy anecdotes are all well and good, but can we consolidate our understanding with mathematical rigour? Using some Bayesian statistics this is indeed possible (an excellent book on the topic for newcomers to the area can be found here).
We start with the idea that, given two events (A and B), we know that if we are given information for one of these events, A say, then we can calculate the probability of event B happening given the information of A. We denote this \mathbb{P}[B|A] . A special formula, known as Bayes’ theorem, then states the following with this information:
\mathbb{P}[B|A]=\frac{\mathbb{P}[B]\mathbb{P}[A|B]}{\mathbb{P}[A]}We apply this to Monty Hall problem as follows. In this problem we have three doors 1,2,3 and we have the events that the prize lies between each respective door, denoted D_1, D_2, D_3. Lets suppose we select door 1 initially, and our host Monty opens door 3 to show a goat. So it follows that \mathbb{P}[D_3] =0.
Now let G be the information that there is a goat behind door 3. We can use Bayes’ Theorem to formulate the following probabilities for finding the Car behind doors 1 or 2, given the information of G, as:
\mathbb{P}[D_1|G]=\frac{\mathbb{P}[D_1]\mathbb{P}[G|D_1]}{\mathbb{P}[G]}, \\ \\ \mathbb{P}[D_2|G]=\frac{\mathbb{P}[D_2]\mathbb{P}[G|D_2]}{\mathbb{P}[G]}We can calculate the probabilities of each quantity of the Right hand side intuitively as:
\mathbb{P}[D_1]=\mathbb{P}[D_2]=1/3 \\ \mathbb{P}[G|D_1]=1/2 \\ \textrm{(As, if the prize was behind door 1, we can choose either 2 or 3 to open)} \\ \mathbb{P}[G|D_2]=1 \\ \textrm{(As we are just restricted to opening door 3 if the prize is behind 2)}\\ \mathbb{P}[G|D_3]=0 \\ \textrm{(If the prize lies here, we can’t open it)}Since D_1, D_2, D_3 cannot occur simultaneously, then, we can use some more simple statistical properties, specifically mutually exclusivity to express the probability of a goat behind door 3 as:
\mathbb{P}[G]=\sum_{i=1}^3 \mathbb{P}[D_i]\mathbb{P}[G|D_i]=(1/3)(1/2)+(1/3)(1)+(1/3)(0)=1/2Placing all these values back into our Bayes equations yields:
\mathbb{P}[D_1|G]=\frac{\mathbb{P}[D_1]\mathbb{P}[G|D_1]}{\mathbb{P}[G]}=\frac{(1/3)(1/2)}{1/2}=1/3, \\ \\ \mathbb{P}[D_2|G]=\frac{\mathbb{P}[D_2]\mathbb{P}[G|D_2]}{\mathbb{P}[G]}=\frac{(1/3)(1)}{1/2}=2/3.Hence, if we switch to door 2, it gives us a 2/3 chance of winning and staying with door 1 produces a 1/3 chance.
Numerical Simulation
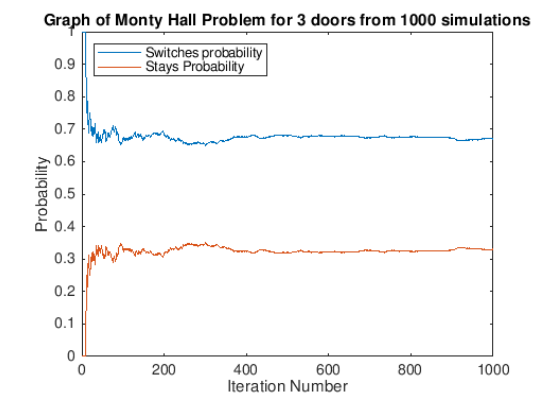
Unfortunately I couldn’t think of a witty title for this section, but nevertheless it would still be interesting to explore a simulation and see if we can back up these theoretical results. To do this, we run the monty hall problem 1000 times, randomly generating where the car lies, which door we open and the probability of winning if we stay or switch. We should see that switching means we win about 66.6% of the time and the plot below, showing the aggregated probabilities as we run the simulation more times, support our Bayes based theory.
And with this, we close our first show. In the next blog post we explore some extensions to this problem, and answering the burning question: what if Monty Hall had access to more doors, more goats, and more contestants?
Further Reading
For another take on the Monty Hall problem, see this by a fellow STOR-i student.
