It may or may not come as a surprise to you that the majority of banknotes in the UK have traces of cocaine on them. Contamination on this scale makes it difficult to determine whether cash can be associated with drug dealing or not. In particular, discriminating between traces of cocaine found on banknotes used in general circulation compared with those used in illegal drug activity is a key area of interest. The purpose of this blog post is to give a brief insight into the work of scientists at the University of Edinburgh, whose work aims to illuminate the value of using the quantity of cocaine on cash as criminal evidence.
Data
Tandem mass spectrometry data are available for banknotes taken from general circulation as well as those seized from criminal investigations. The data recorded consist of a series of peaks for the cocaine product ion m/z 105, with each peak corresponding to an individual banknote. The area under each peak was measured and its logarithm was used as a measure of the quantity of cocaine on each banknote.
In particular, two datasets are considered. The first dataset consists of samples of banknotes obtained from criminal cases where the defendant was convicted of a drug crime involving cocaine. It is important to note that banknotes in this dataset are likely to exhibit two different types of cocaine contamination:
- A level of contamination consistent with that typically observed in general circulation. Perhaps these notes were not contaminated during the crime and instead these notes exhibit a similar level of contamination as that ‘fiver in your pocket’.
- A level of contamination consistent with illegal drug activity involving cocaine.
Clearly, one would expect the level of contamination in the first instance to be lower than that of the second. The second dataset we consider consists of banknotes taken from a variety of locations around the UK. These banknotes are highly unlikely to contain whole samples that are associated with illegal activity and therefore should exhibit similar contamination as described in point 1 above.
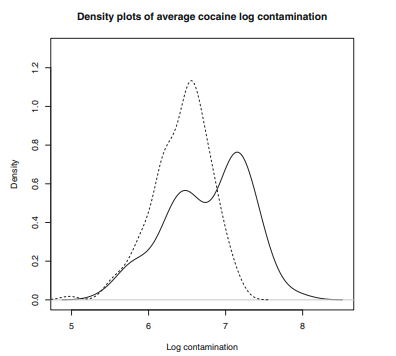
The plot below illustrates the overlap in mean quantities of cocaine from samples taken from both datasets. We refer to the first dataset as the criminal case data and the second as the general circulation data. It is interesting to note the bimodal (meaning it consists of two peaks) nature of the criminal case data, which appears to be consistent with the two types of contamination described above.
So how do we quantify the evidence relating to cocaine on banknotes?
The value of the evidence can be quantified by use of a likelihood ratio. In statistics, the likelihood ratio expresses the likelihood of the evidence under two competing propositions. It is essential to evaluate to what extent the contamination supports a particular proposition relative to another so as to provide a measure of the meaning and probative value of the evidence. The propositions to be considered in this case are:
- H_c : the banknotes are associated with a person who is associated with a criminal activity involving cocaine.
- H_d : the banknotes are associated with a person who is not associated with a criminal activity involving cocaine.
The likelihood ratio associated with these propositions is given by:
LR = \frac{f(\mathbf{z} | H_c)}{f(\mathbf{z} | H_d)}where the function f is a probability density function for the measurements \mathbf{z} , conditional on H_c and H_d respectively. We denote by \mathbf{z} = (z_1, \dots, z_n) the logarithmic transformation of the measurements of the peak areas of cocaine found on a set of n banknotes (i.e. the data used in the analysis) . If the likelihood ratio is greater than 1, then the evidence provided by the sample is said to assign more support to the proposition that the banknotes are associated with criminal activity involving cocaine.
An Example of a Statistical Model
A number of statistical models can be used to estimate f , some of which assume independence among the quantities on the n banknotes in a sample. However, it is somewhat unreasonable to assume that the quantity of cocaine on one particular banknote is unaffected by the quantity of cocaine on its immediate neighbouring banknote in a sample. Therefore, it makes sense to consider a model which allows for a measure of association between quantities of drugs on adjacent banknotes.
An approach of this nature was developed by Amy Wilson at the University of Edinburgh who fitted Auto-regressive models of order one (AR(1) models) to the data. The main advantage of using AR(1) models was that they were able to account for the autocorrelation that arises due to the fact that cocaine is very sticky and therefore easily transferable to adjacent notes in a sample. When compared to previously developed models which assumed independence, these models performed better. Details of such methods can be found in the references at the end of this blog post.
Further Reading
While the AR(1) model worked relatively well, more sophisticated methods were developed to account for the fact that different samples of banknotes from criminal cases often have a mixed level of contamination. More specifically, the notes come in batches from various drug users which are then bundled by dealers. Consequently, different bundles have different levels of contamination.
Researches subsequently proposed a hidden Markov model to account for the uncertainty regarding which bundles notes are in. The purpose of this more sophisticated approach was to enable the modelling of the differences in contamination between different bundles of notes. More information regarding this model and other statistical methods discussed in this blog can be found below:
The evaluation of evidence relating to traces of cocaine on banknotes – Amy Wilson, Colin Aitken, Richard Sleeman, James Carter
The evaluation of evidence for auto-correlated data in relation to traces of cocaine on banknotes – Amy Wilson, Colin Aitken, Richard Sleeman, James Carter