I recently spent the weekend back in Edinburgh (my home town). Whilst I was there, I went to see the Royal Scottish National Orchestra (RSNO) in concert at the Usher Hall. The night was in honour of John Williams who has composed some of the most popular, recognizable, and critically acclaimed film scores in cinematic history. I can’t quite describe the feeling of hearing live music on this scale after a long 2 years. With scores like Star Wars, Superman, E.T. the Extra-Terrestrial, Jaws, Schindler’s List and Saving Private Ryan, it truly was an incredible night.
Listening to these incredible film scores in this full-scale symphonic tribute got me thinking…is there a mathematical way to write music? So, I did a bit of digging around on the internet, and turns out there is!
Whilst there seems to be no evidence of the legend John Williams using mathematical methods to create his music, there is evidence out there to suggest that other composers such as Mozart, Beethoven and Debussy (to name a few) used the Fibonacci Sequence to write their sonatas.
What is the Fibonacci Sequence?
Put simply, the Fibonacci Sequence is a series of numbers which commonly starts at 0 and 1, and in which each number is the sum of the two preceding numbers:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610…
In mathematical notation we can describe the Fibonacci Sequence as X_{n} = X_{n-1} + X_{n-2}.
The golden ratio, denoted by \phi , in decimal form is approximately 1.618033988… When dividing each term by its previous term in the Fibonacci Sequence, the golden ratio can be seen in the answer. Furthermore, this value becomes more accurate as we get farther into the sequence. For example: 13/8 = 1.625; 89/55 = 1.1818; 610/377 = 1.61803; and so on, converging to 1.618033988… . This golden ratio is what is commonly known as “The Divine Proportion” due to its frequency in the natural world.
Squares with the dimensions of the Fibonacci Sequence can be arranged in a spiral pattern:
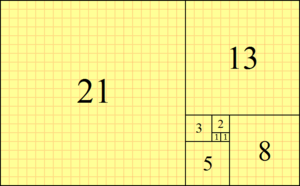
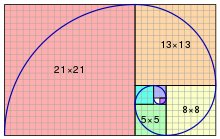
The corners of each square can be connected by quarter-circle arcs to form the Fibonacci spiral:
This sequence, pattern and spiral presents itself in many things you may never have noticed before. For example, it is used in art and music:
The Fibonacci Sequence in Music
The Fibonacci Sequence is an integral part of Western harmony and music scales. Some examples are given below:
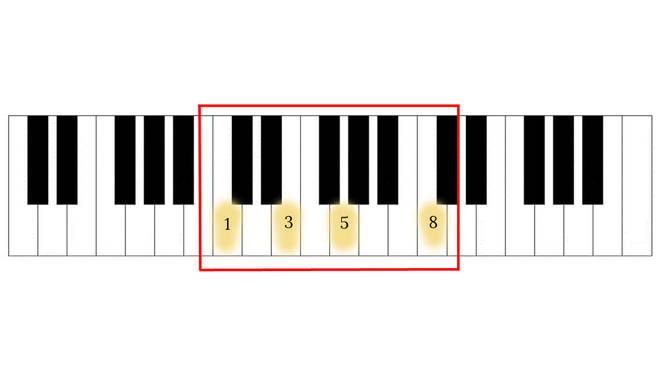
- An octave on the piano consists of 13 notes: 8 white keys and 5 black keys
- A scale consists of 8 notes, of which the 3rd and 5th notes make up a basic chord
- In a scale, the dominant note is the 5th note, which is also the 8th note of all 13 notes that make up the octave
- 8 divided by 13 equals 0.61538… the approximate Golden Ratio
Note: these are all numbers which feature in the Fibonacci Sequence: 0, 1, 1, 2, \bold{3, 5, 8, 13}, 21, 34, 55, 89, 144, 233, 377, 610…
The Fibonacci Sequence in Action
Composers have been using the Fibonacci Sequence and the Golden Ration for hundreds of years to compose amazing music. For example, many of Mozart’s piano sonatas are based on the Golden Ratio.
A sonata is traditionally made up of 3 parts: exposition, development and recapitulation, in which the musical subject matter is stated, explored or expanded, and repeated.
It transpires that Mozart arranged his piano sonatas so that the number of bars (a bar is a small segment of music that holds a certain number of beats) in the development and recapitulation divided by the number of bars in the exposition would equal approximately 1.618, the Golden Ratio.
This can be seen in many of Mozart’s works, but as an illustrative example we take the first movement of his Piano Sonata No. 1 in C Major.
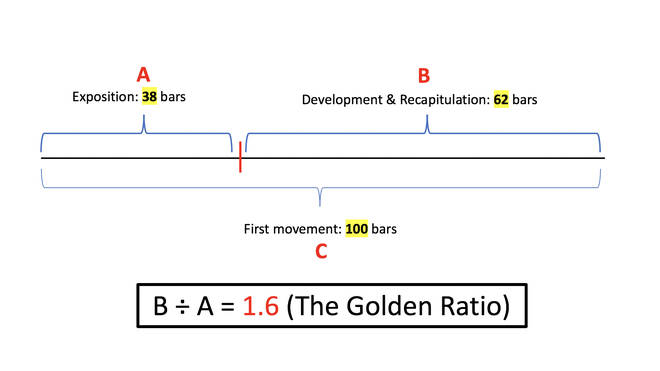
In the diagram above, C is the sonata’s first movement as a whole, B is the development and recapitulation, and A is the exposition.
The exposition has 38 bars and the development and recapitulation has 62. The first movement as a whole contains 100 bars.
62 divided by 38 equals 1.63 (approximately the Golden Ratio).
The Golden Ratio has also been used in other areas of music including being used to craft violins, saxophones mouthpieces, and in speaker wires.
Perhaps a more up-to-date example of its usage involves singer-songwriter Lady Gaga. Her song ‘Perfect Illusion’ contains a particularly bold key change at the 111-second point. By putting the key change at this specific spot (i.e. 111 out of 179 seconds) she nailed the Golden Ratio sweet spot, 1.618. Check it out here.
Further Reading (and watching)
This blog has only scratched the surface in terms of the mathematical theory behind a lot of the concepts discussed. Check out this report for a more in-depth review.
This video shows how a piano piece can be composed using the Fibonacci Sequence by assigning numbers to the E major scale.