It is thought that around one in two people in the UK will get cancer at some point during their lifetime, and around two thirds of all those who get cancer are likely to undergo a course of radiotherapy as part of their treatment.
Technological advances in recent years have enabled the customisation of treatment plans for individual patients based on their unique anatomy and cancer type. However, one particular challenge that remains in the planning process is the ability to create a plan in which radiation is effectively delivered to cancerous cells while sparing surrounding healthy tissues. The conflicting nature of these goals makes the planning process difficult, and over the years a number of multi-objective optimisation methods have been developed in an attempt to address this problem.
While multi-objective methods have proved particularly effective in dealing with, and exploring the trade-off between these conflicting goals, the vast majority of cancer centres worldwide use a planning system based on single objective optimisation methods, often involving a weighted sum of conflicting objectives. The intended purpose of this blog post is to demonstrate how multi-criteria decision-making methods can be used to assess the quality of treatment plans, assuming that they have been generated by available commercial treatment planning systems.
The Treatment Planning Process
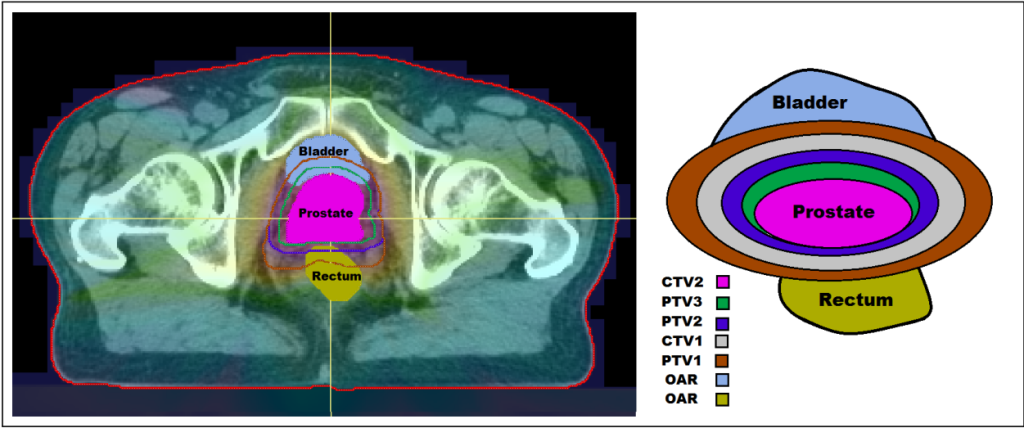
The initial stages of radiotherapy treatment planning involve medical imaging techniques such as Computerised Tomography (CT) scans in order to identify the size, shape and location of the tumour, as well as any surrounding healthy organs at risk (OARs). Following this, clinicians determine planning target volumes (PTVs) which define the target doses of radiation to be delivered to certain cancerous cells. Before a treatment plan can be approved for delivery, various criteria need to be met. These criteria are encoded in what is known as a clinical protocol. Plans that fail to meet the criteria set out in the protocol may have to be re-optimised using a trial and error process. This trial and error aspect of the planning process is inefficient and time consuming, often leading to the acceptance of plans which do not achieve the full potential of the available technology.
Data Envelopment Analysis
One possible way in which to evaluate the quality of radiotherapy treatment plans is by using a management science technique called Data Envelopment Analysis (DEA).
Traditionally, DEA is used to evaluate a set of decision-making units (DMUs) that convert inputs into outputs. Specifically, DEA evaluates the efficiency of each DMU by comparing it to all other DMUs, in search of any improvements. In this blog post, we will focus on the input-orientated DEA model which searches for possible improvement of a DMU via proportional reduction of its inputs. In a loose economic interpretation, the inputs represent the cost we pay for producing outputs.
In the context of radiotherapy, the DMUs are the treatment plans, the inputs are the doses delivered to the OARs and the outputs are the doses to the PTVs. Thus, DEA assesses how well a treatment plan performs in terms of delivering the prescribed dose to the tumour while limiting the dose delivered to OARs. The overall goal is to determine whether a plan is efficient among a set of plans for the same cancer type treated at the same treatment centre using the same treatment protocol (to ensure comparability).
The DEA Model
We assume that there are I DMUs, each with N inputs and M outputs. All data representing the I DMUs are contained in the input matrix \bold{X} \in \mathbb{R}^{N\times I} and output matrix \bold{Y} \in \mathbb{R}^{M\times I} in which the i^{th} column contains the data for the i^{th} DMU. The DEA model to evaluate the i^{th} DMU is the linear optimisation problem
\textrm{minimise} \quad \ \ \theta^i \\ \textrm{subject to} \quad \bold{Y}\lambda - y^i \geq0 \\ \quad \quad \quad \quad \quad \ \bold{X}\lambda - \theta^i x^i \leq0 \\ \quad \quad \quad \quad \quad \ e^T\lambda = 1 \\ \quad \quad \quad \quad \quad \ \lambda \geq0.
In this model x^i and y^i are the i^{th} columns of matrices \bold{X} and \bold{Y} respectively. We note that \theta^i \in \mathbb{R} and \lambda \in \mathbb{R}^I are both decision variables, and e \in \mathbb{R}^I is simply a vector of ones.
A DMU is considered efficient if the optimal value of this linear optimisation problem \theta^{i∗} = 1 . An optimal value other than 1 indicates that it should be possible to proportionally decrease the inputs, while at the same time keeping the same output level. In the context of radiotherapy, the data available for the I plans suggest that we can improve the i^{th} plan by reducing radiation dose to the OARs without decreasing the dose delivered to the PTVs.
Furthermore, for treatment plans classified as inefficient, the model identifies a subset of plans that in combination have features that outperform the current plan, therefore providing guidance on how the current plan should be improved. More details of this can be found in the references below.
Further Considerations and Reading…
While DEA offers many advantages as a quality assessment technique, it is not without its limitations. For example, it relies on the assumption that the radiation dose delivered to the body is exactly the same as that specified in the treatment plan. However, this is very rarely true in practice. One reason for this is that the relevant structures receiving radiation can move (ever so slightly) over time. Therefore, there are often discrepancies between the planned and delivered dose.
As such, the method of DEA can be enhanced by considering data uncertainty in the treatment plans. Methods such as uncertain DEA have been described in the literature, or more recently, techniques involving simulation. It has been observed that some treatment plans classified as inefficient by DEA can achieve efficiency should a sufficient amount of uncertainty be considered.
The main takeaway from these methods is that if an inefficient treatment plan requires a small amount of uncertainty to evaluate as efficient, then this is likely not a bad treatment plan, but is in fact the by-product of imprecise data. However, a plan requiring high levels of uncertainty to evaluate as efficient indicates that further improvement is required via re-planning.
Further information on these developments and traditional DEA is provided in the links below.
Mathematical optimization in intensity modulated radiation therapy – Matthias Ehrgott, Cigdem Guler, Horst W. Hamacher, Lizhen Shao
Evaluating the Quality of Radiotherapy Treatment Plans for Prostate Cancer – Emma Stubington, Matthias Ehrgott, Glyn Shentall, Omid Nohadani
Uncertain data envelopment analysis -Matthias Ehrgott, Allen Holder, Omid Nohadani
Introduction to Data Envelopment Analysis and Its Uses: with DEA-Solver Software and References – William W. Cooper, Lawrence M. Seiford, Kaoru Tone