The situation for kidney transplants is somewhat different to that of other organs – since humans only need one kidney to survive, it is possible to recieve a kidney from a living donor. Transplants from live donors are preferable, since they typically have a higher chance of success than a transplant from a deceased donor. Many patients are able to find a willing donor (a family member, for example) but such a transplant can only take place if the patient and donor are compatible. If this is not the case, a kidney exchange can be arranged – for example, a paired exchange where two patient-donor pairs exchange donated kidneys.
Given a large number of incompatible patient-donor pairs, can we organise a large scale kidney exchange so that as many patients as possible recieve a compatible kidney? This idea was suggested by Roth, Sönmez, and Ünver in 2002, who derived a solution from the work of Gale and Shapley on matching problems. Roth and Shapley jointly won the Nobel prize in economics in 2012 for their contributions to the field.
We’ll start by looking at the stable marriage problem, a simple matching problem solved by Gale and Shapley in the 1950s. We’ll then reformulate the problem for the kidney donation setting and look at how to solve it using similar ideas.
The Stable Marriage Problem
The formulation of the stable marriage problem as originally solved by Gale and Shapley is as follows: we wish to play matchmaker between a group of n women and one of n men. The individuals in each group would like to marry a member of the other, and have a personal preference order on members of the other group. The aim is to produce a matching (bijection) between the two groups that is stable, i.e. where there is no pair who are not married under the matching who mutually prefer each other over their current spouses.
Gale and Shapley showed that such a matching always exists, and can be constructed with the Gale-Shapley algorithm, in which members of one group propose to their favourite candidates, who provisionally accept the best offer made to them.
To illustrate this, we’ll look at a simple example with 6 people.
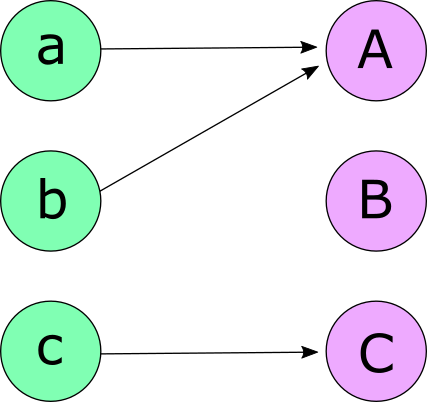
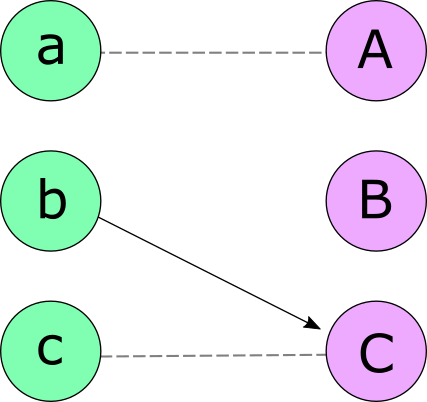
First, the men propose to their first choices, and the women who recieve a proposal provisionally accept the one from their favourite suitor. In this case, a and b both propose to A, who decides to accept a. C accepts her only suitor, c. The rejected men then propose to their second choices – here b must make a second proposal, to C this time.
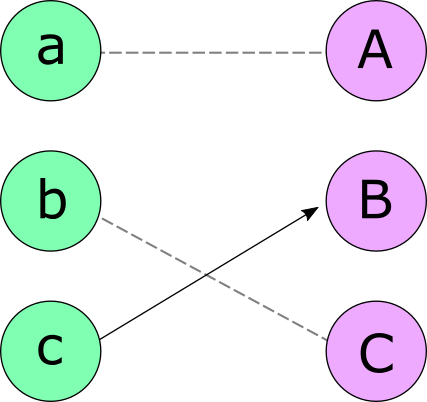
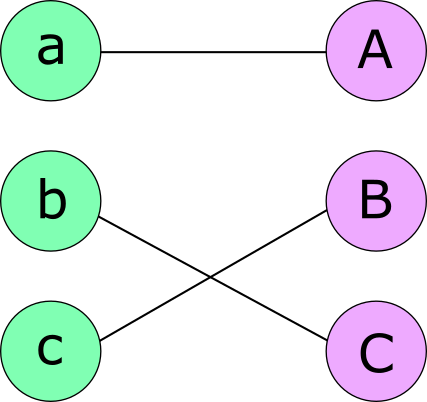
The process repeats until everyone is engaged, with C accepting the new proposal from b and c finally being engaged to B.
The algorithm always terminates and constructs a valid matching, since men do not propose to the same woman more than once and everyone is compatible with every member of the other group. The resulting matching is also always stable – for example, if b prefers A to his current partner he must have proposed to her at some earlier stage and been rejected in favour of someone she liked better, so A must like her current partner more than b.
The Kidney Exchange Problem
This matching problem has some similarities to the stable marriage problem – we want to establish a matching between a group of n kidney donors and n patients in need of transplant, and each patient has a preference order on kidneys according to compatibility.
There are some additional complications, however – not every kidney is compatible with every patient (this is why the patient-donor pairs cannot simply perform a direct exchange). This means it may not always be possible to match every patient to a live donor – if a compatible kidney is not currently available, a patient may choose to instead be given a high priority spot on the waiting list in exhange for their donor’s kidney. The donors themselves do not have any preferences about where their donated kidney goes, but will not donate it unless their partner recieves a kidney or a high priority spot on the wait list in exchange.
The problem setup is as follows: each patient has a preference list, reflecting their preferences over the set of kidneys compatible with them and ending in w if the patient and donor are willing to exchange their kidney for a priority place on the waiting list. w is always last on the preference list since transplant from a compatible living donor is always preferable. A kidney exchange occurs as a cycle (a closed loop where each kidney is donated to the previous patient in the cycle) or a chain ending in w (where the last member of the donation chain accepts a spot on the waiting list). Roth et al. presented the following algorithm (called the Top Trading Cycles and Chains or TTCC algorithm) to solve this problem, building on work by Gale and Shapley.
Each pair first points to their first choice of kidney. We represent this as a directed graph with arrows pointing from each pair to the pair with their chosen kidney. If a cycle is formed then all members of cycle are removed and their transplants can take place. If no cycle was formed then the longest chain ending in w is selected (with ties broken by e.g. patient priority) and the corresponding transplants can take place. The free kidney belonging to the first pair in the chain is left available for selection.
This process then repeats, with pairs selecting their second (third,fourth…) preferences if their first has been removed from the system. At each stage it is guaranteed that at least one cycle or chain will be formed. The process terminates when either all patients have left the system, or when all patients remaining in the system have exhausted their list of options, in which case they may choose to wait for the next exchange to be run. Unclaimed kidneys (found at the start of a w-chain) are donated to patients on the waiting list.
To illustrate this we will consider a simple example with 7 patient-donor pairs.
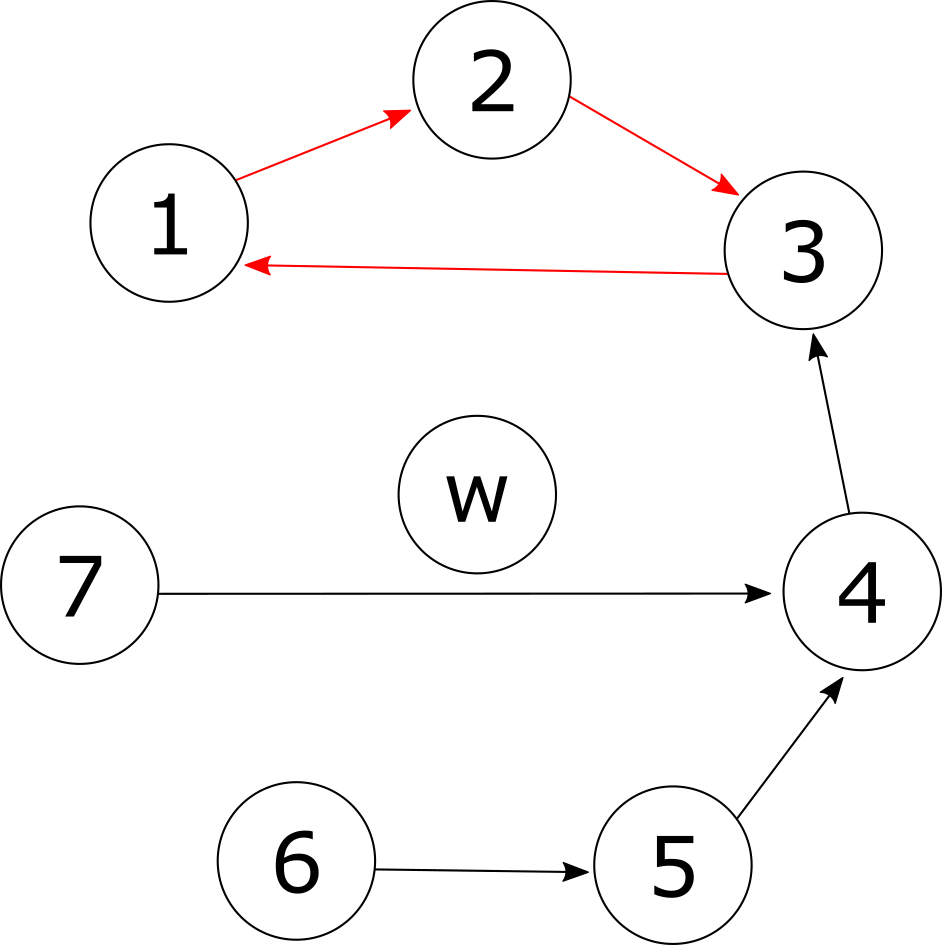
In the first round, each patient points to their first choice of kidney. A cycle has formed (highlighted in red), so patients (and kidneys) 1, 2 and 3 can immediately leave the system and take part in transplants.
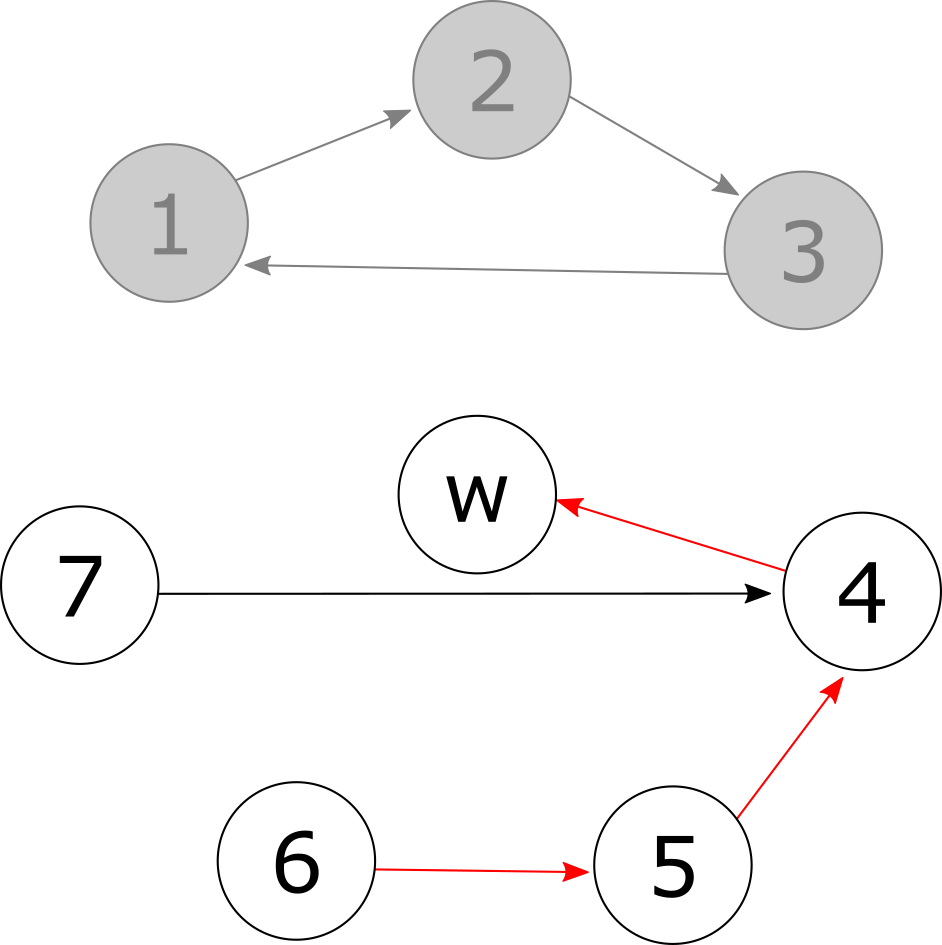
Next, patient 4 must select their second choice – in this case, no more compatible kidneys are available and they settle for a spot on the waiting list. A w-chain is formed (highlighted in red) and patients 4, 5 and 6 can leave the system, although we have yet to decide what to do with donor 6’s kidney.
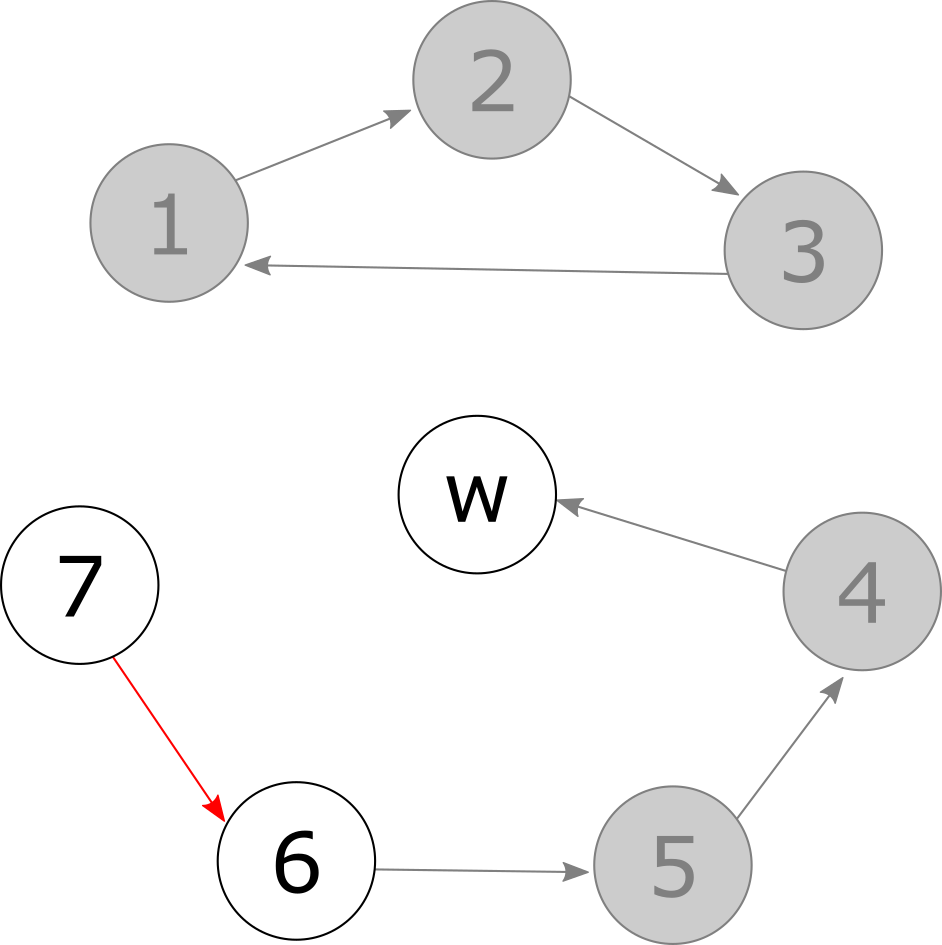
In the next round patient 7 chooses their next best available choice (donor 6’s kidney) and the w-chain from earlier can be extended.
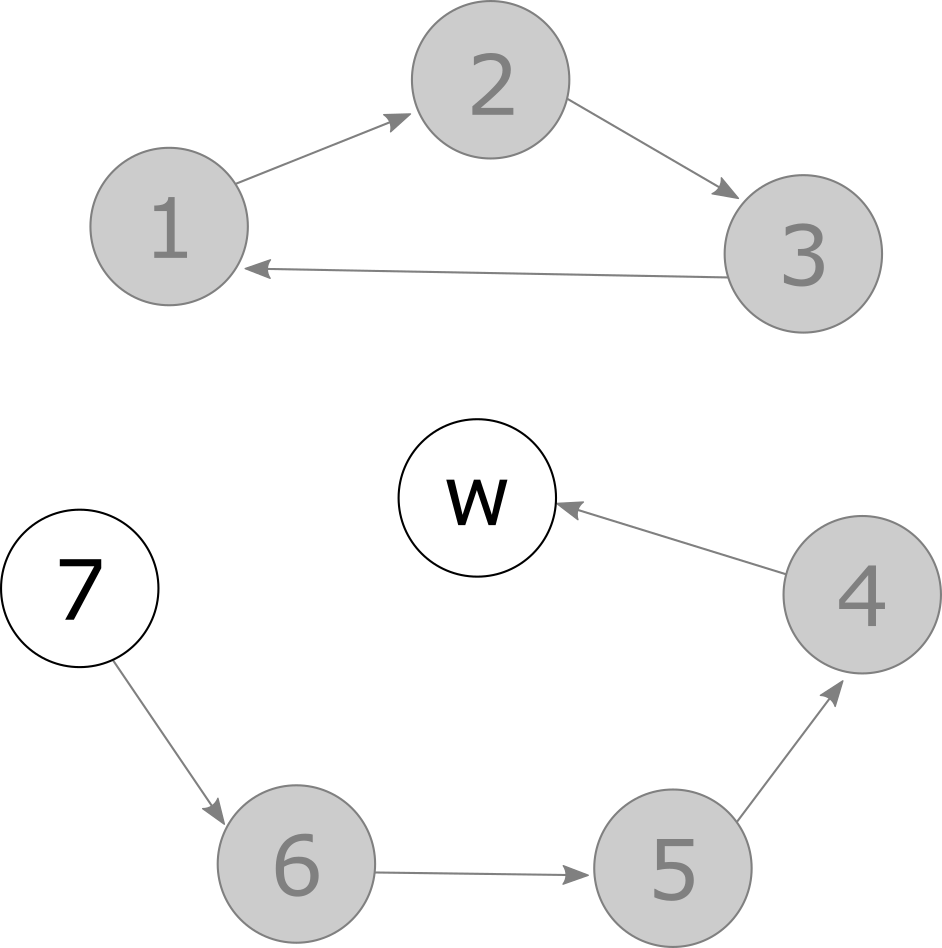
Finally, all patients have been allocated a kidney or a spot on the waiting list. The remaining kidney from donor 7 will be given to the highest priority compatible patient on the waiting list.
This algorithm does not always result in a matching for all patients and donors, but it does always result in a matching that is Pareto efficient – there is no other matching that is better for some patients without being worse for others. Hence the matching is stable in the sense that no other would be unanimously preferred by all patients, and no subgroup can all improve their situation by coming to a different agreement amongst themselves. The algorithm is also strategy-proof – no patient can achieve a better outcome by lying about their preferences.
Further Reading
- How an economist helped thousands get a new kidney – Ian Rose
- The theory of stable allocations and the practice of market design. The Nobel Prize in Economics 2012 for Alvin E. Roth and Lloyd S. Shapley – Jordi Massó
- College Admissions and the Stability of Marriage – D. Gale and L. S. Shapley
- Kidney Exchange – Alvin E. Roth, Tayfun Sönmez, M. Utku Ünver