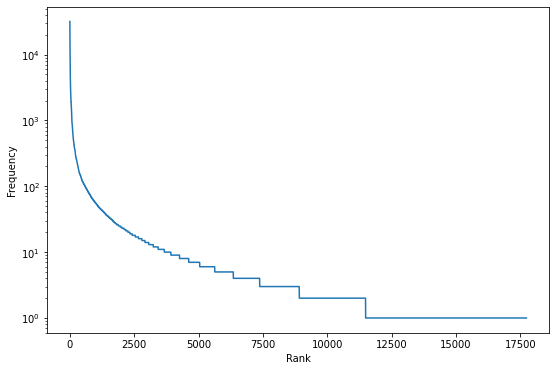
The key issue in using text data is the sheer number of words we have to learn about! To make matters worse, we do not have the same amount of information about each word. This is because the relative frequencies of words are incredibly skewed – in a given corpus, only a small number of words will make up the majority of the word count. We’ll illustrate this with an example corpus: the Sherlock Holmes series. This has a total word count around half a million, with just over 17500 unique words. The sorted frequencies for each word are plotted below, and you can already see that the distribution is heavily skewed towards the more common words. In fact, the 100 most common words make up almost 60% of the total word count, while half of the words in the vocabulary appear only once or twice.
This issue persists even for very large text corpora (the Oxford English Corpus has 2 billion words and the top 100 words still make up half of that count), and causes enormous problems for dealing with text data since we have lots of information about a handful of words and only a little about the rest. Modern language models usually handle this problem by being careful about how they choose to represent words. Simple methods treat each word as its own distinct entity: a string of characters or an index in a dictionary. In reality, though, words are related to each other, and a more informative representation would capture similarities and differences in word meanings.
Word embeddings (or word vectors) are representations of words as points in a vector space, where words with similar meanings are represented by points that are close together. This reduces the dimensionality of text datasets and makes it possible to transfer knowledge between words with similar meanings, effectively increasing the amount of data we have about each word.
Example – Food Vectors
To illustrate this, an example of how you might consider representing foods as points (or vectors) in 2d space:

Here, I’ve decided the two key pieces of information about any foodstuff are temperature (hot/cold) and state (solid/liquid). This places meals that you’d consume in similar situations close together in space. If we measure vector similarity by the cosine similarity (the cosine of the angle between them), we can compute a score for how similar certain words are on a scale from 1 (same meaning) to -1 (opposite meanings). In our example, similarity(soup,stew) = cos(10) = 0.98, while similarity(soup,salad) = cos(180) = -1.

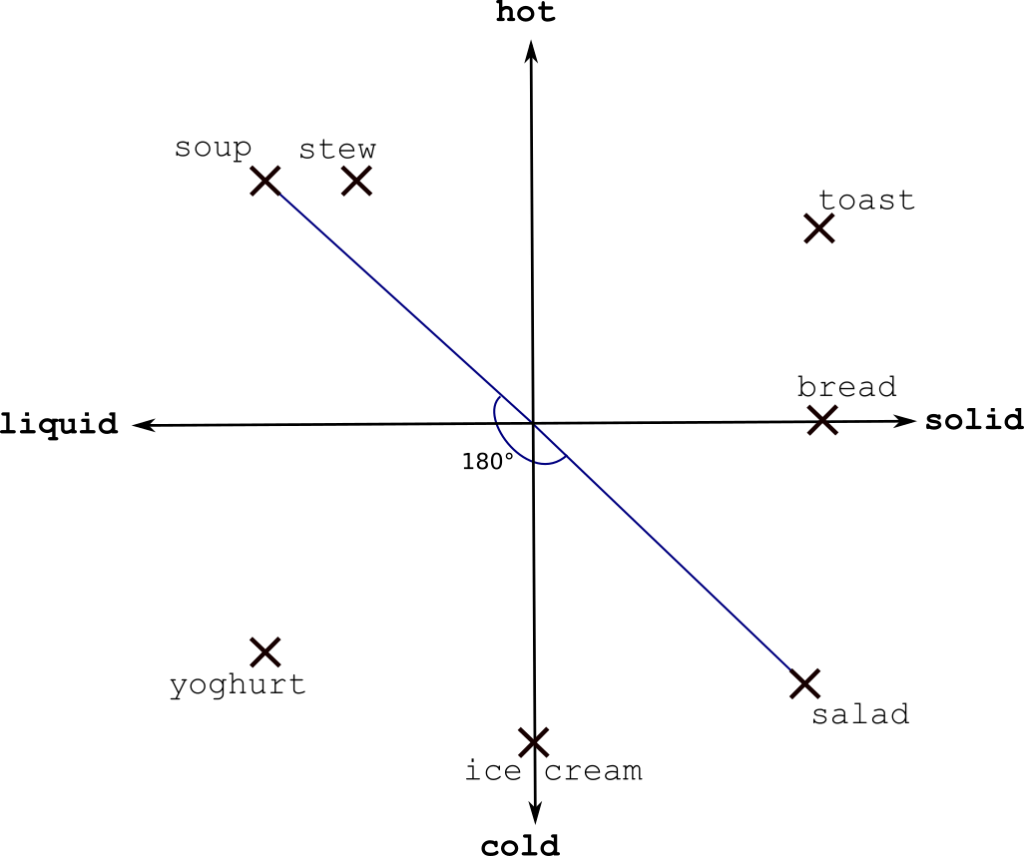
This representation also gives rise to some interesting observations, since mathematical operations like addition and subtraction have natural definitions for vectors. For example, considering the words as vectors gives sense to the sum “yoghurt – cold + hot”, which has the answer…
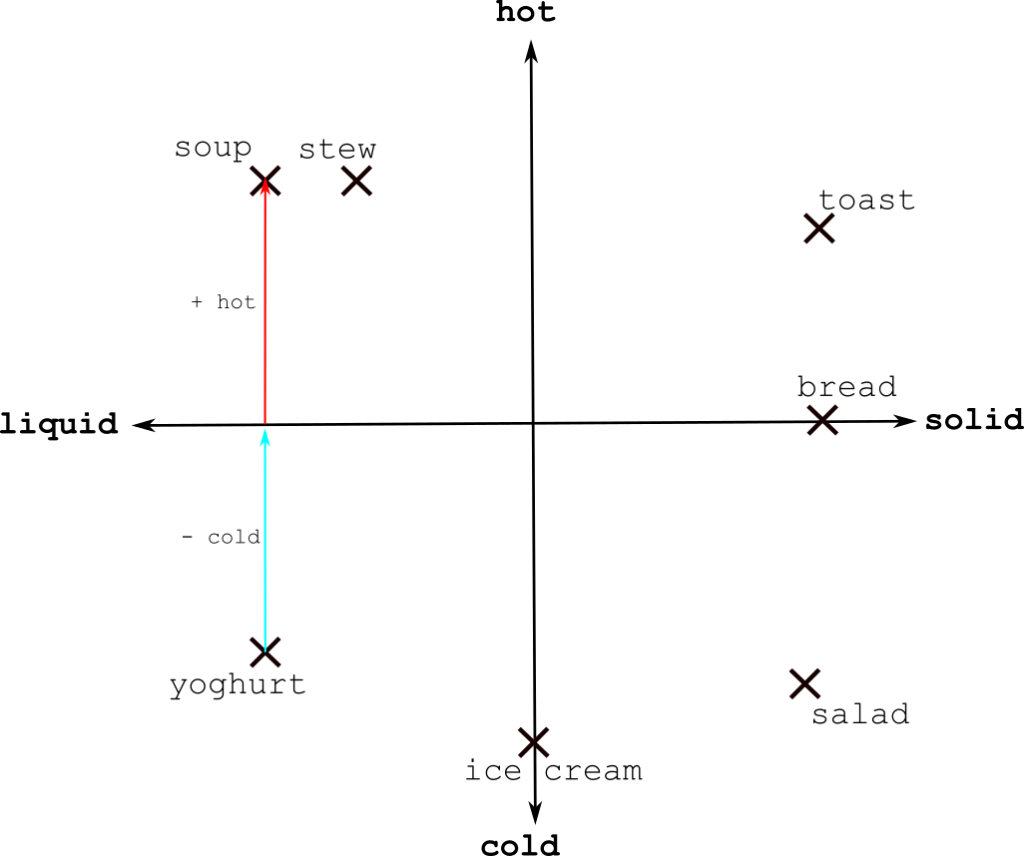
soup.
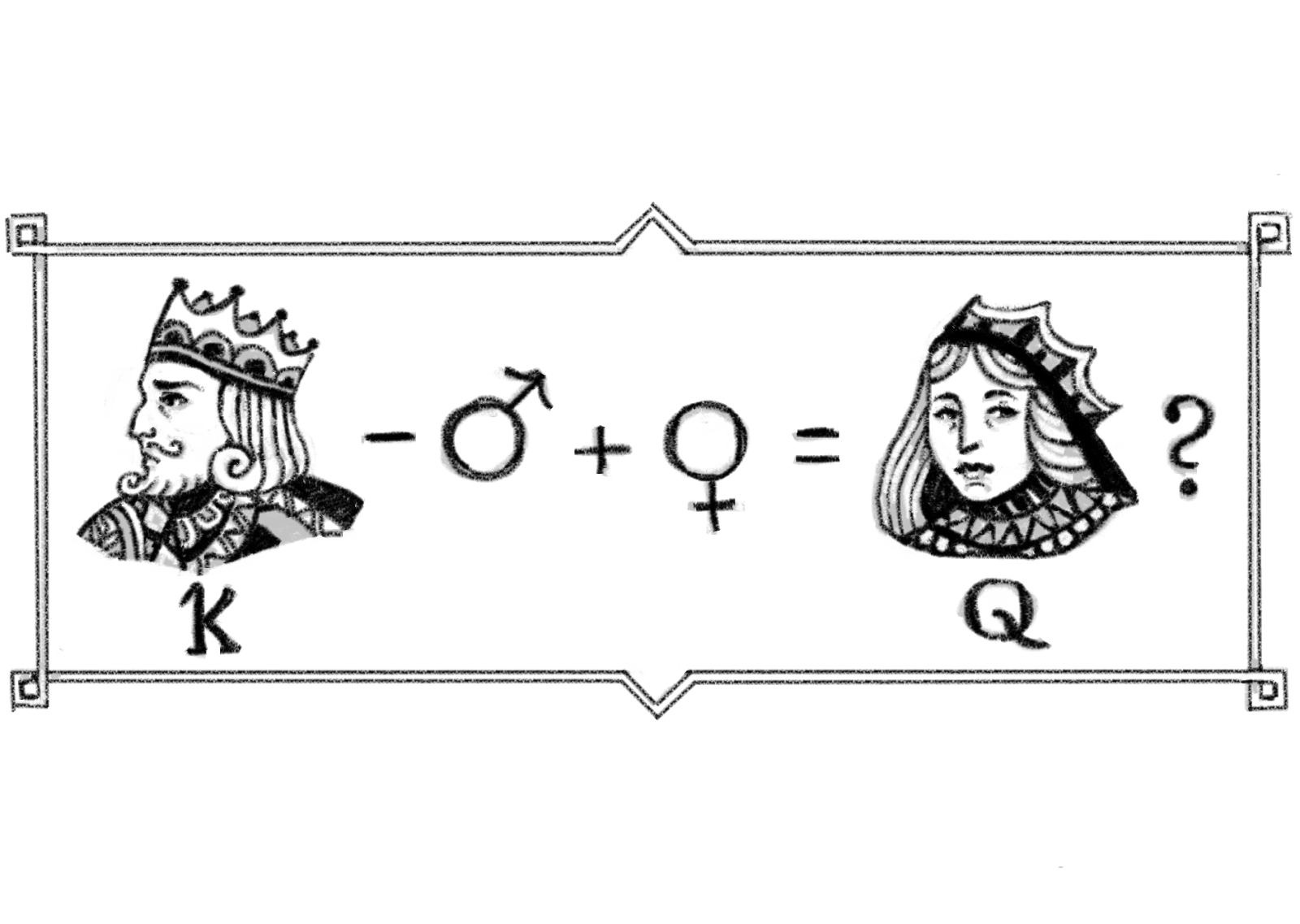
Obviously, this representation is not perfect (is there a meaningful difference between soup and hot yoghurt?), but it’s not hard to imagine that if we increased the number of dimensions – by adding on extra directions like sweet/savoury, for example – it would be good enough to represent most of the meaningful differences and similarities between foods. In practice, when we use a model to learn word embeddings, the individual co-ordinates do not correspond to easily understood concepts like they did in the example above. However, we can still find interesting linear relationships between words: relationships like “king – man + woman = queen” still hold, and directions can be found that correspond to grammatical ideas like tense, so that “eat + <past tense> = ate”.
word2vec
The key question now is how to find such a representation! This is usually done by training a model for some classification task that is easy to evaluate, and using the resulting fitted parameters as word embeddings. Perhaps the most famous example is word2vec. In its “skip-gram with negative sampling” variant, the prediction task is to estimate how likely any given two words are to appear near each other in a sentence. The motivation here is that words are likely to have similar meanings if they appear in similar contexts – if I tell you “I ate phlogiston for dinner”, you’ll be able to tell from context (proximity to the words ate and dinner) that phlogiston is most likely a food and could hazard a guess at how it would be used in other sentences.
We can easily get positive examples from the text by taking pairs of words that did appear near each other, and negative examples by randomly selecting some noise words. The embeddings are fitted to maximise classification accuracy on this dataset, and the model is designed so that the resulting embeddings have high cosine similarity if the words they represent appear in similar contexts.
We’ll use the Sherlock Holmes corpus again as an example, using the Gensim implementation for python to learn 100-dimensional word vectors. The results are more easily visualised by projecting them into 2 dimensions with principal component analysis – the resulting projection preserves some of the structure of the vector space, including some clusters of similar words. See below for a visualisation of 100 common words from the dataset:
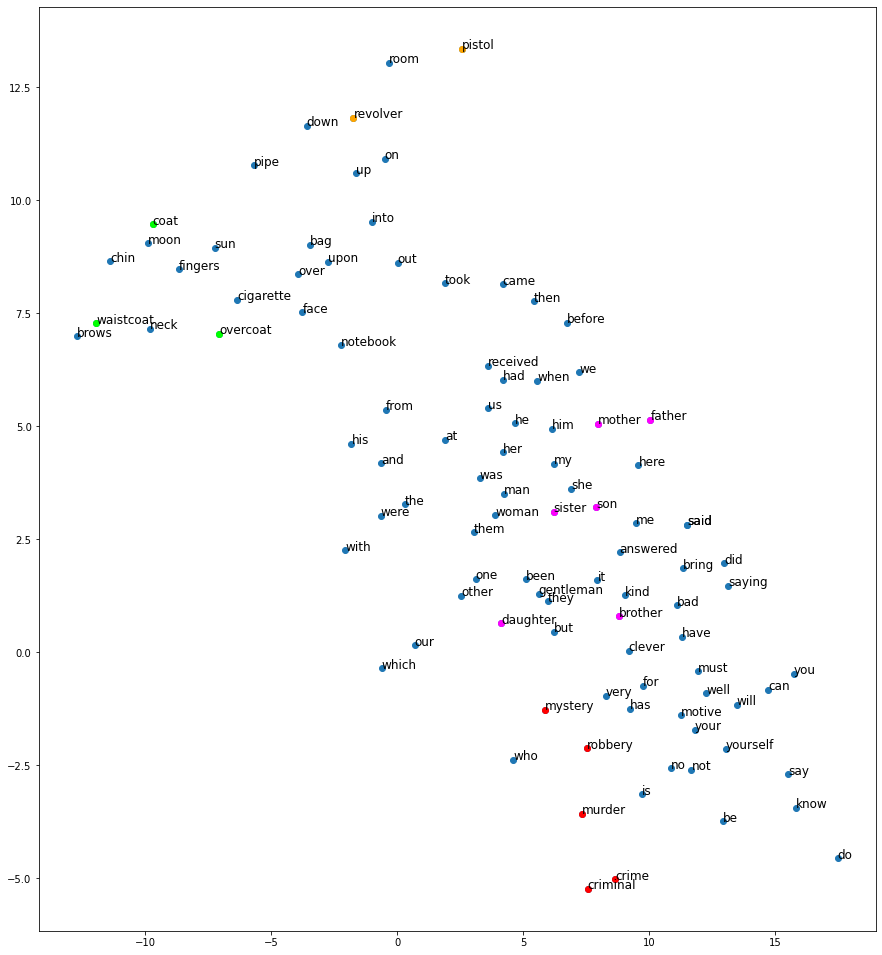
Some clusters of words with high cosine similarity have been highlighted. The model did well at grouping words with similar meanings together – some examples are listed in the table below. The model was also reasonably successful at grouping words by syntactic meaning – nouns, adjectives, and verbs were usually grouped together, with verbs even grouped by tense as well as meaning.
| Word | Most similar to: |
|---|---|
| you | ye (0.85), yourselves (0.83) |
| say | saying (0.87), bet (0.85) |
| said | answered (0.88), cried (0.83) |
| brother | father (0.88), son (0.88) |
| sister | mother (0.93), wife (0.92) |
| coat | overcoat (0.94), waistcoat (0.94) |
| crime | murder (0.87), committed (0.85) |
| holmes | macdonald (0.76), mcmurdo (0.75) |
Of course, those were the highlights of this particular set of embeddings – this corpus is actually on the small side so the semantic similarities found for some words were complete nonsense. The most useful thing about word embeddings, however, is how transferable they are across corpora – it is common to use word embeddings trained on a big corpus in a language model for a small corpus, and many sets of pre-trained word embeddings are available for this purpose.
An interesting property of word embeddings is that the embedding spaces for different languages often share a similar structure – embeddings trained with word2vec for different languages have a similar geometric structure, and it is even possible to learn a linear map between the embedding spaces that allows for translation of words. The matrix for this map can be trained using a list of translations for some common words, and the resulting projections are surprisingly effective at translating words, even allowing for the detection of errors in a translation dictionary.
Further Reading
- Speech and Language Processing (Chapter 6: Vector Semantics and Embeddings) – Dan Jurafsky and James H. Martin
- Statistics and Data Science for Text Data – Connie Trojan (my dissertation)
- Distributed Representations of Words and Phrases and their Compositionality – Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg Corrado, and Jeffrey Dean
- Exploiting Similarities among Languages for Machine Translation – Tomas Mikolov, Quoc V. Le, and Ilya Sutskever