Simultaneous Inference in Clinical Trials

As part of my undergraduate study I completed a dissertation titled “Simultaneous Inference in Clinical Trials” supervised by Dr Fang Wan. In particular I focused on the construction of simultaneous confidence intervals for treatment effects. In this post I wanted to share with you a brief overview of some of my findings.

Within clinical trials it is common to test multiple hypotheses simultaneously. This is referred to as multiple comparisons. An example of where this arises is in biomarker trials. Biomarkers are measurable indicators of biological conditions that can be used to identify target populations within trials.

Example – Biomarker trials have the following set up: as patients are enrolled onto the trial their biomarker status is identified; these results are used to stratify individuals into two groups: biomarker positive or biomarker negative. From here, patients are allocated treatments using randomization. In this case we consider a two-treatment scenario in which we are testing a new treatment (T) against a control (C). This control is usually either an existing treatment which we wish to show is inferior or equivalent to the new treatment, or it is a placebo, which is a drug identical to T but lacks the active agent. The stratification process is illustrated in the figure below. This design creates four subgroups within which we simultaneously estimate the size of the treatment effect (i.e. the result of a specific treatment within a subgroup).

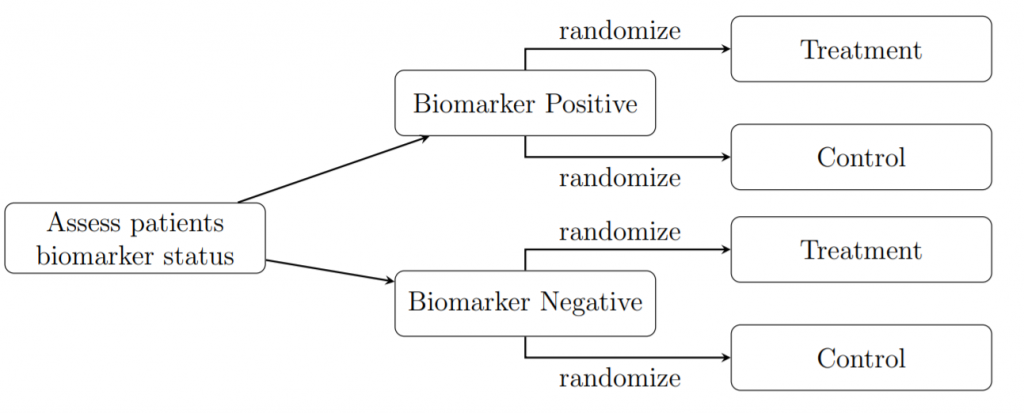
We will be focusing on trials with binary endpoints i.e. the treatments were either deemed a success or failure. Therefore, our parameter of interest is the proportion of times the treatment was successful.

Before we delve into the issues associated with multiple comparisons we need definitions of the error rates that will play a significant role in simultaneous testing.

Type I Error: Occurs when we reject a true null hypothesis. The type I error rate is the probability of making a Type I Error. This is equivalent to the significance level which we often set to be \(\alpha\)=0.05.

Type II Error: Occurs when we accept a false null hypothesis. The type II error rate is the probability of making a Type II error.

Confidence Interval: A confidence interval (CI) is constructed to demonstrate the degree of uncertainty surrounding a parameter estimate. These intervals have confidence level \(1-\alpha\) when a large number of intervals are constructed and \(100(1-\alpha)\)% contain the true parameter value.

Family-Wise Error Rate (FWER): The probability of rejecting at least one true null hypothesis.

When conducting simultaneous hypothesis tests, we are often interested insuring that the significance level for a whole group of hypothesis is \(\alpha\), rather than just at the individual test level. To do so we need to control the FWER to be approximately \(\alpha\).

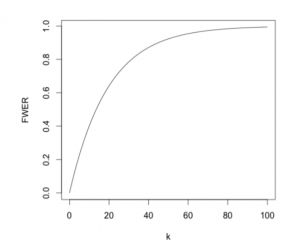
If we are testing \(k\) independent hypothesis simultaneously, their overall FWER is given by $$\text{FWER}\;=\;1-\mathbb{P}(\text{No true null hypothesis rejected})\;=\;1-(1-\alpha)^k.$$ Therefore, as the number of hypothesis increases, the error rate rapidly tends to 1, meaning the probability of making at least one type I error rises to an unacceptable level as demonstrated by the following figure.

I will now discuss two ways in which to correct for multiple testing.

Bonferroni Correction

When using Bonferroni correction, we set the significance level for an individual hypothesis test to \(\alpha/k\) where \(k\) is the total number of hypotheses being tested simultaneously. We reject the \(i^{th}\) hypothesis when the p-value is less than \(\alpha/k\).

With Bonferroni applied, the family-wise error rate is kept equal to, or below \(\alpha\). As the FWER can be below the desired significance level, we call it conservative. It becomes increasingly conservative as the number of hypotheses increases (as seen in the figure below).

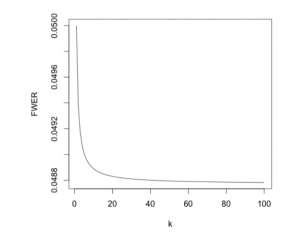
If the independence assumption for the FWER is not met, Bonferroni could become extremely conservative. A family-wise error rate below 0.05 will lead to a greater number of null hypotheses being accepted despite being false. Thus, we’ve improved the type I error rate at the expense of the type II error rate.

Sidak Correction

Like Bonferroni, Sidak correction involves adjusting the significance level of an individual test in order to control the FWER. This time we set the significance level for an individual hypothesis test to \(1-(1-\alpha)^{1/k}\).

When testing several independent hypotheses simultaneously the use of Sidak correction ensures that the FWER is exactly \(\alpha\). This is a more powerful method than Bonferroni as it is always less conservative. However, this is reliant on the fact that the hypotheses are independent. If any dependencies do arise Sidak can be overly liberal and produce a FWER greater than \(\alpha\), giving an unacceptably high probability of making a type I error.

Because of this reliance on the independence assumption, we tend to prefer the Bonferroni method. To add to this, despite Sidak having greater statistical power, the improvement over Bonferroni is minimal.

Within my dissertation I used these methods and others to construct several different types of simultaneous confidence intervals, determining which was optimal under varying conditions. Although I won’t go into the ins and outs of this in this blog posts, I will share that Bonferrnoi correction with a Wilson Score interval did give optimal coverage and length properties, regardless of the sample size, number of hypotheses being tested and the value of the parameter estimate.