Clustering!

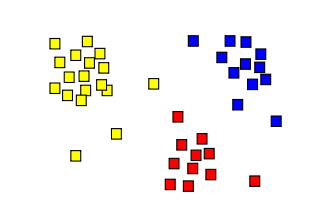
I don’t know about any of you but to me clustering feels like a foreign concept, at least in the physical sense. Just over a year into a global pandemic, the image of a group of people being in close proximity feels like an alternative reality you’d only see in a sci-fi movie. The only kind of clustering I can be apart of these days is the statistical kind. Not quite as exciting as a mosh pit but arguably more productive. In the statistical sense, clustering is essentially grouping data together based on similar features. These similarities can be anything, depending on the data you are dealing with, from book genres to people’s heights to the types of crime committed in a particular area and just about everything in-between. This statistical analytic technique, found commonly in Machine Learning, is comprised by a number of algorithms. In this post, we’ll take a look at two of these methods.

First, let’s dive into an unsupervised learning algorithm called K-Means clustering. The algorithm for K-Means clustering is relatively simple and goes like this:

1. Choose a number of clusters.
2. Place the same number of central points in different locations.
3. For each data point, evaluate the distance to each centre point. Classify the point to be in the cluster whose centre is closest.
4. Re-compute the cluster centre by taking a mean of all the vectors classfied to that cluster.
5. For each data point, re-evaluate the distance to each centre point. And re-classify the point to be in the cluster whose centre is closest.
6. Repeat steps 4 and 5 until the change in cluster centre is sufficiently small.

K-means clustering has the advantage that it works fast but there is a couple of drawbacks. The randomness of the cluster centres also means that the K-means clustering can fall short in terms of consistency. If we were to repeat the process we may not see the same results. Also, the algorithm requires the specification of the number of clusters before we can begin, which in some cases can be hard to figure out.

So, what else is out there? Well, there is also agglomerative hierarchical clustering. It may be a mouthful but it doesn’t require a specification of the number of clusters before the algorithm can start – woohoo! Agglomerative hierarchical clustering is what’s called a bottom-up algorithm which means it treats every single data point as a cluster to begin with. Then, as we move through the process, pairs of clusters merge. The hierarchy of clusters can be shown as a tree where the root is the cluster that contains all the data points.

The algorithm follows these steps:

1. Treating all data points as a single cluster, define a metric for the similarity between two clusters.
2. Merge the two clusters with the largest similarity.
3. Repeat step 3 until there is only one cluster containing all data points or stop when the number of clusters is desirable.

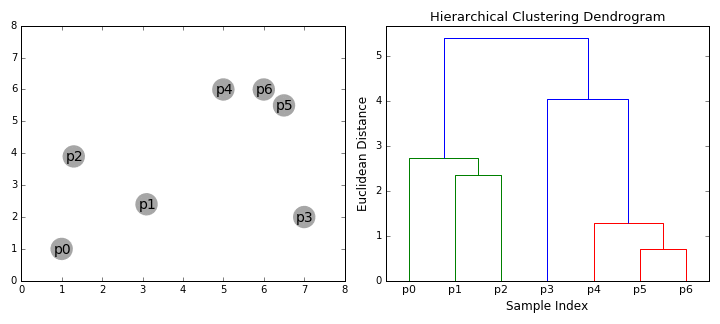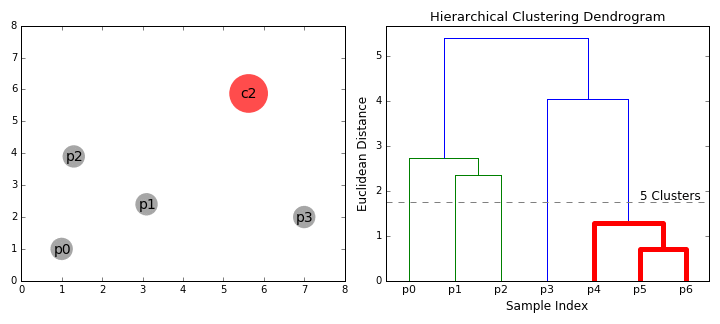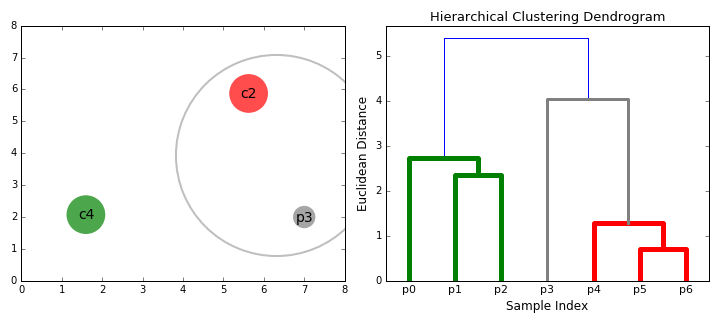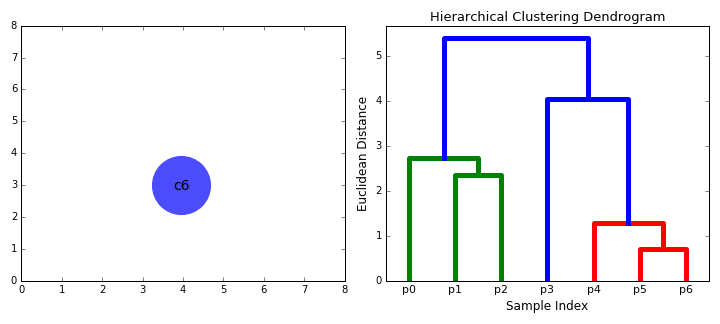
There are a number of difference metrics available of calculating the similarity between clusters and thus which clusters to merge. The centroid method merges the clusters with the most similar average point of all points in a cluster. Alternatively, Ward’s method merges clusters that minimize variance measured by the sum of squares index.

Agglomerative hierarchical clustering gives the freedom for a user to choose a point to stop when the number of clusters look satisfactory. Additionally, various similarity metrics tend to work well for this algorithm. However, unlike K-mean clustering, which has linear complexity, this method has complexity O(n³). So it isn’t as efficient.

Clustering methods are important in data mining and machine learning communities and form a powerful statistical technique. I hope this blog post brings together (I swear I don’t find the puns, the puns find me) some of the key info about clustering for you. Look down below for where to go to learn more and check back soon for more blog posts.

Now it’s time for my tweet of the week! This week’s goes to @ProfMattFox!

Missed my last post? Check it out here.

Want to know more?

Discovering similarities across my Spotify music using data, clustering and visualization | by Juan De Dios Santos | Towards Data Science

Agglomerative Clustering – Statistics How To

Gan, G., Ma, C. and Wu, J., 2020. Data clustering: theory, algorithms, and applications. Society for Industrial and Applied Mathematics.