Can MCMC Be Updated For The Age Of Big Data?
17th January 2016
On Friday I attended a STOR-i Seminar, the first of the new year. These sessions are a chance for
STOR-i students to share their work with the rest of the group. It's a really good way of keeping in touch with what everyone
else is doing, and the questions afterwards have the potential to suggest different ways of looking at the problems. It was
Jack Baker's turn to talk about how his PhD is progressing. He is considering ways to
speed up Markov Chain Monte Carlo (MCMC) processes in order to deal with modern world statistics.

The world is constantly throwing data at us at a terrifying rate. But how can statisticians handle this information onslaught?
Are tools such as MCMC, a particular favourite, up to the new challenges of dealing with such large masses of data? This is the
focus of Jack's work. The
problem with MCMC is that it involves calculating the likelihood, $f(\mathbf{x}|\theta)$, which for large
amounts of data has a huge computational cost. Jack has been testing a few alternative approaches to speed up MCMC.
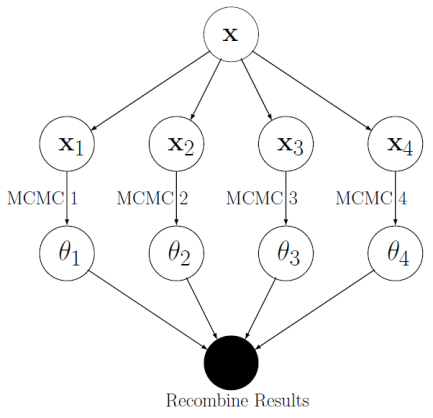
The first idea he considered was parallelisation of MCMC. What if we split the data, $\mathbf{x}$ into $S$ batches $\mathbf{x}_{B_1},...
,\mathbf{x}_{B_S}$? The posterior distribution (spoken about in my first blog, STOR-i
Conference 2016) can be split into $S$ factors.
$$p(\theta|\mathbf{x}) \propto \prod_{i=1}^Sp(\theta)^{1/S}f(\mathbf{x}_{B_i}|\theta)\propto \prod_{i=1}^Sp(\theta|\mathbf{x}_{B_i}) .$$
Now MCMC can be applied to the individual batches at the same time, but on different processors (see diagram). The different
samples can then be recombined somehow to give a full data set. The recombination techniques considered were Kernel Density
estimates and Gaussian methods.
These methods seem to perform reasonably well until it comes to posteriors with multiple modes. At this point, the methods
are rather inaccurate, and almost always completely miss the two distinct peaks. Some of them simply put the peak in at the
true saddle point.
The next method he used for performing Bayesian Inference on large data sets was Stochastic Gradient Hamiltonian MC (SGHMC).
This uses the gradient of the posterior to come up with a good proposal, $q(\theta)$, to sample from. This tends to give very
high acceptance rates for samples from $q(\theta)$ and can be tuned such that the acceptance rate is effectivley 1. This
allows the
acceptance step to be left out, saving a great deal of computational time. Moreover, when tuned well, SGHMC
actually performs quite well, and was actually able to pick out multiple modes in a posterior when they exist. This is a vast
improvement over the parallelisation methods described earlier.
However, SGHMC also has its drawbacks. One is that the are currently no efficient algorithms to tune it. As the tuning is vital
to its appeal and manual tuning is very difficult, Jack is unsure how useful SGHMC will be in the immediate future. On top of
this, it requires storing the entire data-set in the memory at once. Sometimes this simply isn't feasible.
Due to these problems, Jack still sees a place for parallelised MCMC in the near future. However, there need to be some big
improvements. One suggestion he made was to ensure that under recombination, the distributions were given heavier tails. We can
only really wait and see how successful they prove to be, or whether the necessary improvements to methods like SGHMC take place
first.