The vast majority of cancer centres worldwide use commercial systems based on single objective optimisation methods to formulate treatment plans for radiotherapy patients. In my last blog post, I discussed how data envelopment analysis could be used in conjunction with expert opinion from skilled radiologists to assess the quality of such plans, before they were approved for use.
However, in an ideal world, the planning process would involve specialised computer systems based on multi-objective optimisation methods. It is thought that these systems, coupled with input from expert practitioners, would be better able to deal with and explore the trade-off between the inherent conflicting goals of radiotherapy. That is, providing enough radiation to destroy cancerous cells whilst simultaneously sparing surrounding healthy organs at risk (OARs).
Intensity Modulated Radiation Therapy (IMRT)
IMRT is a particular type of radiotherapy in which patients are secured to a bed, and beams of radiation are fired at the cancerous cells from various angles using a linear accelerator and a collimator. The linear accelerator provides the radiation and the collimator controls the dose distribution.
The radiation is passed through a multi-leaf collimator (MLC), a device consisting of a number of pairs of metal leaves moving along channels into the path of the radiation to block out areas of the beam. By moving the leaves into different positions, improved beam shaping can be achieved, allowing the beams to fully concentrate on the cancerous cells to be irradiated.

There are 3 main problems to be considered when designing a treatment plan for IMRT patients. These are:
- How many beams should be fired at the patient, and from what angle?
- What intensity should these beams be fired at?
- How do we administer this intensity via the MLC?
In this blog post, I will discuss the mathematical challenges involved in the first problem. Further information on the second and third problems can be found on a fellow STOR-i students blog page here.
Beam Angle Optimisation (BAO)
The first of the problems identified above is formally known as the beam angle optimisation (BAO) problem. This involves determining the angles at which radiation should be delivered via the accelerator. This is particularly important in situations that are anatomically difficult. For example, when a tumour is intertwined in some healthy organ or if the tumour has a nonconvex shape.
Selecting the beam angles is traditionally done manually by an expert clinician. This often requires several trial and error iterations which is both time intensive and subject to the experience of the clinician. Conversely, using optimisation methods to identify beam directions would remove the dependence on the clinician’s experience and speed up the planning process.
The linear accelerator used to provide the radiation is capable of rotating 360^{\circ} around a point, called the iso-centre. While this can be viewed as a positive in the sense that there are no restrictions on the angles available, it also means that there are infinitely many angles to choose from. This increases the difficulty of selecting the best set of beam angles since it is impossible to try every possible combination in order to find the optimal set.
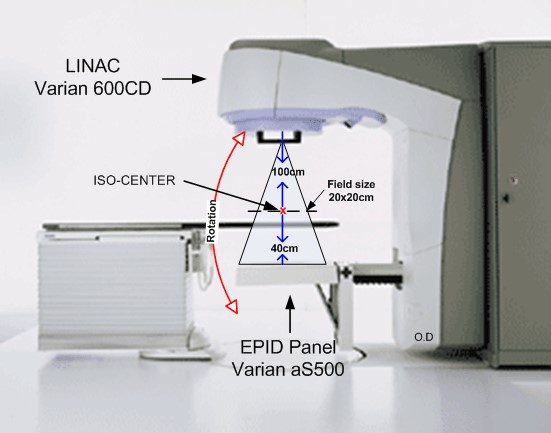
One way in which this problem has been addressed is via what is known as an “exhaustive search”. This strategy involves selecting a pool of n equally spaced angles, from which we will consider m combinations of angles. As a toy example, consider choosing m = 7 angles from the set
n=\{0^{\circ}, 10^{\circ}, \dots, 400^{\circ}.\}
While this considerably reduces the number of angles required for consideration, it is still very large. Specifically, there are over 20 million ways to choose 7 angles from the above set (i.e. 41\choose{7} = 22,481,940). Therefore, it is hard to know how much to reduce the number of angles for consideration by. It is also easy to see that this strategy could be rather time consuming.
Once a choice has been made regarding which angles to use, there is a need to evaluate this choice before it is approved as part of the treatment plan. For example, we might want to compare various groups of angles and decide which is best for treatment. In order to evaluate these “groups” a simplified version of the next stage in the process, known as the fluence map optimisation (FMO) problem, is conducted. More information on the FMO is provided in the references below. Put simply, we find the objective value of the FMO problem for each group, and this value (which can be though of as a “score”) is compared with other plans. Again, this can be a rather time intensive process depending on the values of n and m .
It has been shown that many near-optimal plans will not vary much in score. Hence, we can consider groups of beam angles to be equally good if their score lies below (or above depending on the FMO method) some pre-determined threshold.
Further Reading
Further information on how to solve the BAO problem using the “exhaustive search” approach can be found here.
Blog posts by STOR-i student Matthew Davison relating to the second and third problems in the planning process are given below:
- What intensity should these beams be fired at? (FMO problem)
- How do we administer this intensity via the MLC? (LSO problem)
An alternative to the exhaustive search strategy outlined in this blog post is the “Gradient Search Approach”. More information can be found here.