In Mathematics, often you don’t have a neat formula for the things you want to calculate. However, you can sometimes use an algorithm to get an answer that’s as close as you want, for example finding the root of an equation by rearranging it in your calculator and then pressing the = sign a lot of times.
These algorithms usually have starting values, and picking the wrong starting value can affect how long the algorithm needs to run to get a ”good enough” answer. But what if you didn’t need to pick a starting value or an amount of time to run the algorithm, and it just gave you the exact right answer? This report examines one way to do this, called Coupling From The Past or CFTP for short.
Instead of running our algorithm into the future (where no matter how long we run it we’ll always be a tiny bit away from the true answer), CFTP asks us to pretend that our algorithm has been running for an infinite time in the past up until now. It then finds out where we would be if that was the case. Since the algorithm has been running for an infinitely long time, it turns out we must be exactly at the right answer. CFTP works by considering every single possible starting value, and then tries to make them ”couple up” to end up at the same place as quickly as possible by fiddling about with the random numbers the algorithm uses. Then it doesn’t matter where the algorithm started from infinitely far in the past, because all the roads lead here!
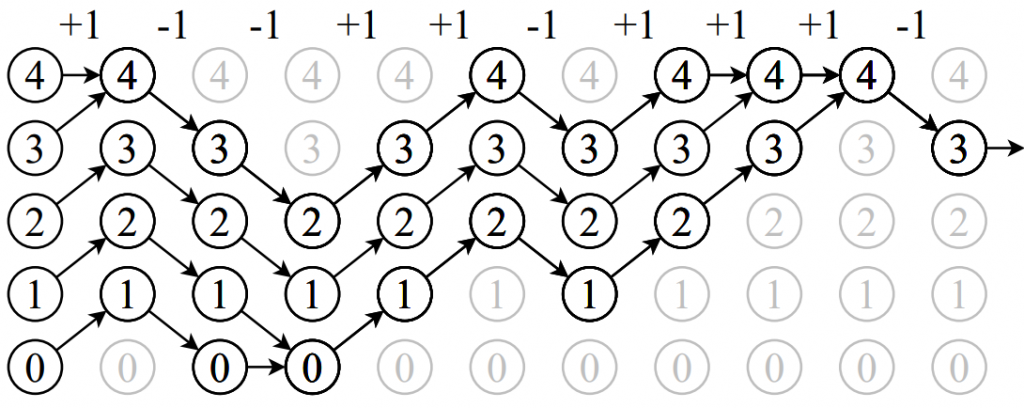
CFTP is quite a tricky method. It only works for some algorithms and needs to have random numbers, and running something ”from the past” is a lot harder to get your head around than running it the normal way. In particular, you need to be very careful where you’re getting those random numbers from, or the end answer won’t be right.
Luckily, we can tell the computer to give us the same random numbers we asked it for a while ago by setting a random ”seed”. Without this, CFTP wouldn’t be possible.
See the creator of CFTP’s website http://www.dbwilson.com/exact/ to get more into the mathematics of this algorithm.