Happy π-day! To celebrate, let’s go all the way back to GCSE maths where we just little baby kids, most likely annoying (at least I was), learning about quadratic equations. Say we want to solve the following quadratic: x^2 – 8x + 12 = 0 Solving this just means we want to find the values of x which makes the entire equation equal to 0. These values are called the roots of the equation. So how do we find the roots of the equation? One method is factorising.
To factorise the above quadratic we want to find two numbers, let’s call them r and s such that we can rewrite the quadratic as x^2 – 8x + 12 = (x – r) (x – s) and r and s satisfy the following properties: r + s = 8 \\ rs = 12
The first property is the sum of r and s equal to 8 not -8 because of the negative signs in the brackets. If we can write our quadratic in this form, as two brackets, then the roots of the equation are r and s. How do we find r and s? Well this is where we’re taught to guess (and when I’ve taught this to students, I told them to guess too, woops). The second property says we multiply r and s to get 12, so that must mean r and s are factors of 12. So we search through all the factors of 12 and find a pair that add together to get 8. Luckily 12 doesn’t have lots of factors so we can see (relatively quickly) that our roots are r = 2 and s = 6. But having to guess isn’t very mathematical, and this method doesn’t work when the roots are quite ugly (involving irrational and/or even imaginary numbers).
So let’s look at this problem differently. Pretend that I didn’t just tell you the answer and we still don’t know what r and s are. Instead of starting with the second property, let’s start with the first. We want two numbers that add together to get 8. Well, if two numbers r and s sum together to get 6, then the average (or mean) of these two numbers will equal 8÷2 = Happy4. If r and s have an average of 4, then that means r and s are equally distanced and on either side of 4.
This means that we can write r and s as r = 4 – d \\ s = 4 + d where d is some number representing the distance r and s are from 4. Now, this is actually great, we have some indication of what r and s are now! If we can just find out what the number d is, then we can just find out what r and s is directly!
So how do we find d? Well, let’s now use the second property but replace r and s with the equations involving d. So we get (4 – d) (4 + d) = 12 If we just expand this, we get 16 – d^2 = 12 Okay, we’re getting somewhere. So rearranging this, we get d = \sqrt{16 – 12} = \sqrt{4} = 2 Now we know what d is, we can put this back into our equations for r and s. This gives us r = 4 – 2 = 2 \\ s = 4 + 2 = 6
And we’re done, yay! But why go through all this fuss when we already have a method for solving quadratics? One reason is because the method before requires us to do a bit of trial and error in order to find the answer and it doesn’t always work on all quadratics. Whereas this method here is more systematic, requires no guess work, and works with all quadratics! But more importantly, this new method gives us a new perspective into what solving quadratics means.
Let’s look at the plot of the above quadratic.
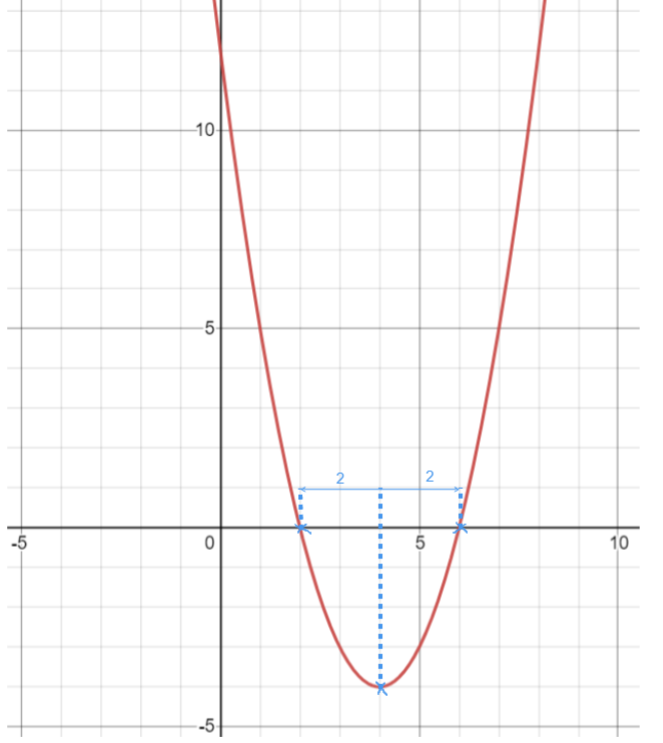
From the plot, we can see that the graph has a value of y = 0 exactly when x = 2 or x = 6, the roots of our equation. But moreover, these roots lie exactly on either side of the point x = 4. Well, when x = 4, the graph is at it’s lowest point. This point is what we call a turning point and for quadratics, everything is symmetric about the turning point. But we already knew that, because our quadratic equals to 0 exactly when our solutions took the form of 4 ± 2, when our solutions are symmetric about 4.
The step-by-step method for solving generic quadratics is below.
We want to solve the following quadratic x^2 – bx + c = 0 To do this, we wish to rewrite this quadratic as x^2 – bx + c = (x – r)(x – s) = 0 where r and s are the roots of the equation. r and s will take the form r = \frac{b}{2} – d \text{ , } s = \frac{b}{2} + d for some number d. Find d by using d = \sqrt{\frac{b^2}{4} – c} Putting this value of d back into the above equations for r and s gives us the roots of the quadratic equation, and therefore we will have solved the quadratic equation.
Exercises
See if you can apply this method on the following quadratics, showing that our method works with whatever quadratic equation given.
So we want to find roots r and s such that x^2 – 10x + 24 = (x – r) (x – s) Expanding this, we can find r and s by using the two equations r + s = 10 \\ rs = 24 Using the first equation, the average of r and s must be equal to 10÷2 = 5. Therefore we have r = 5 – d \text{ , } s = 5 + d for some number d. Putting these equations of r and s into the 2nd property above, we get (5 – d) (5 + d) = 24 \\ 25 – d^2 = 24 \\ d = \sqrt{25-24} = \sqrt{1} = 1 So now we’ve found d. Substituting this value of d into the equations for r and s, we find that our roots are r = 5 – 1 = 4 \\ \text{ and } s = 5 + 1 = 6
So we want to find roots r and s such that x^2 + 7x + 12 = (x – r) (x – s) Expanding this, we can find r and s by using the two equations r + s = – 7 \\ rs = 12 Using the first equation, the average of r and s must be equal to -7÷2 = -3.5. Therefore we have r = -3.5 – d \text{ , } s = -3.5 + d for some number d. Putting these equations of r and s into the 2nd property above, we get (-3.5 – d) (-3.5 + d) = 12 \\ \frac{49}{4} – d^2 = 12 \\ d = \sqrt{\frac{49}{4} – 12} = \sqrt{\frac{1}{4}} = 0.5 So now we’ve found d. Substituting this value of d into the equations for r and s, we find that our roots are r = -3.5 – 0.5 = -4 \\ \text{ and } s = -3.5 + 0.5 = -3
So we want to find roots r and s such that x^2 – 8x + 13 = (x – r) (x – s) Expanding this, we can find r and s by using the two equations r + s = 8 \\ rs = 13 Using the first equation, the average of r and s must be equal to 8÷2 = 4. Therefore we have r = 4 – d \text{ , } s = 4 + d for some number d. Putting these equations of r and s into the 2nd property above, we get (4 – d) (4 + d) = 13 \\ 16 – d^2 = 13 \\ d = \sqrt{16 – 13} = \sqrt{3} We can leave d in this form, perfectly okay! Substituting this value of d into the equations for r and s, we find that our roots are r = 4 – \sqrt{3} \\ \text{ and } s = 4 + \sqrt{3}
So we want to find roots r and s such that x^2 – 8x + 18 = (x – r) (x – s) Expanding this, we can find r and s by using the two equations r + s = 8 \\ rs = 18 Using the first equation, the average of r and s must be equal to 8÷2 = 4. Therefore we have r = 4 – d \text{ , } s = 4 + d for some number d. Putting these equations of r and s into the 2nd property above, we get (4 – d) (4 + d) = 18 \\ 16 – d^2 = 18 \\ d = \sqrt{16 – 18} = \sqrt{-2} = i\sqrt{2} So now we’ve found d. Substituting this value of d into the equations for r and s, we find that our roots are r = 4 – i\sqrt{2} \\ \text{ and } s = 4 + i\sqrt{2} Even when the answer will complex numbers, this method still works!
To answer this question, we first have to get it into a form we are familiar with. To do this, just divide the whole equation by 2. This gets us x^2 – 2x – \frac{5}{2} = 0 We now find the roots r and s such that x^2 – 2x – \frac{5}{2} = (x – r) (x – s) Expanding this, we can find r and s by using the two equations r + s = 2 \\ rs = -\frac{5}{2} Using the first equation, the average of r and s must be equal to 2÷2 = 1. Therefore we have r = 1 – d \text{ , } s = 1 + d for some number d. Putting these equations of r and s into the 2nd property above, we get (1 – d) (1 + d) = -\frac{5}{2} \\ 1 – d^2 = -\frac{5}{2} \\ d = \sqrt{1 + \frac{5}{2}} = \sqrt{\frac{7}{2}} So now we’ve found d. Substituting this value of d into the equations for r and s, we find that our roots are r = 1 – \sqrt{\frac{7}{2}} \\ \text{ and } s = 1 + \sqrt{\frac{7}{2}}
Conclusion
I think this is a pretty interesting take on solving quadratics! Interesting enough to watch a 40min video on this (link to references). Whether we’ll start teaching this to young students, well I’ll just let Secretary of State for Education Gavin Williams decide (spread the word to get this post to him!). If you have any questions or found this to be a good read, feel free to leave a comment or just get in touch!
This blog post was based of a YouTube video I watched by Po-Shen Loh. Check it out here!


