This blog will give an general idea about the principle of particle filter without mathematical proofing.
Recently, we are given talks about particle filter (or sequential Monte Carlo). Particle filter has a wide application in signal processing, tracking objects, time series, finance, etc. In the beginning, I am also scared by the maths of particle filter, like partial differential equations and Bayesian stuff. However, the idea behind the particle filter is very straightforward and intuitive.
Now, lets set a situation to explain it under the tracking problem without mathematics!
Scenario Setting
Assume we are agents of the avengers located in ‘chessboard’ country (that is because the map of this country is like a chessboard 🙂 ). One day Thanos came to this country and said he steal our magic stone and then he just left away and hid somewhere in our city.
Our aim: we are told to trace him before the avengers came.

How to find him?
Luckily, we have three clever dogs named ‘particle A’, ‘particle B’, and ‘particle C’. They have already remembered the smell of Thanos! And we are also clever enough to communicate with them.
Every 10 minutes, they could go head 1 grid in the map based on their own ideas. And then our dogs have to report their location and how likely Thanos come across these areas.
Time=0 minutes
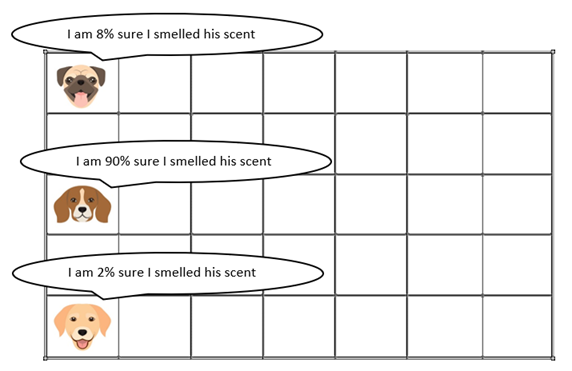
At the beginning, particle B said it is 90% sure there is Thanos’scent. So we think at the beginning Thanos are more likely to go across the middle way.
Time=10 minutes
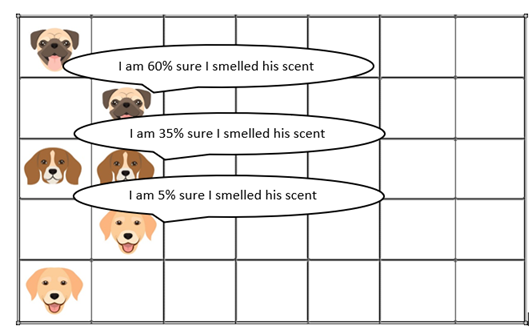
After 10 minutes, our dog moved to new locations and reported their location and their findings. Thanos seems go up from the middle way. as Particle A was 60% sure.
Time=70 minutes
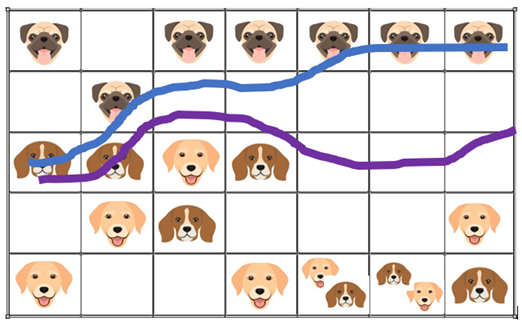
At T=70, we report the most likely route to the avengers (blue line in the figure) based on our three dogs findings. We traced Thanos very well at the beginning. But after T=40, we are far away from his real trace! Finally, our task failed, the avengers could not find him, and he destroyed our world at the end!

Why are we failed? Our dogs are clever, and we are clever. Wait! We track his route very well initially, but after time = 40, particle B and particle C always explore the bottom area. Particle B and particle C said they are not sure Thanos came here, but particle A always said he smelled Thanos’ scent. So we could only rely on Particle A. That’s why we sure Thanos go as particle A’s route.
Particle filter without resampling
The example above illustrates the principle of particle filter without resampling. Each time step, several particles will move follows the transition distribution (like our dogs follow their mind to go head). And based on the evidence (scent of Thanos in our case), we could get the possible location at each time step. Along the time, we could get a trace. However, particle filter without resampling always fails in the long run due to weight degeneracy that the trace is concluded from few particles (In our example, this means we only rely on Particle A after T=40).
Time goes back
Okay, so now the avengers make the time back and we could search again. Particle B and Particle C always explore the locations in the right-bottom corner where Thanos obviously not been there. So let them find those locations is a waste.
New rule: If one of the dogs found Thanos most likely came across their area, we introduce a new dog in this area to pinpoint search. Additionally, if a dog has the least amount of certainty, we remove this dog.
Time = 0 minutes
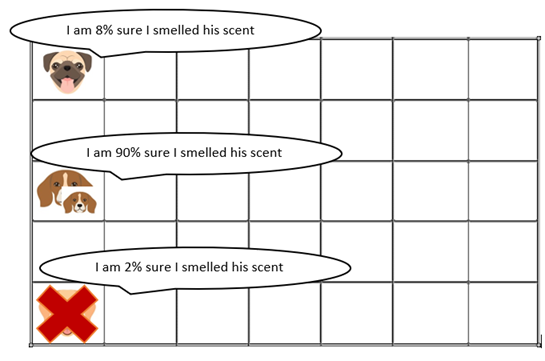
Particle B is 90% sure while Particle C is only 2% sure. So we move particle C and give one more dog on the area where Particle B is.
Time = 10 minutes
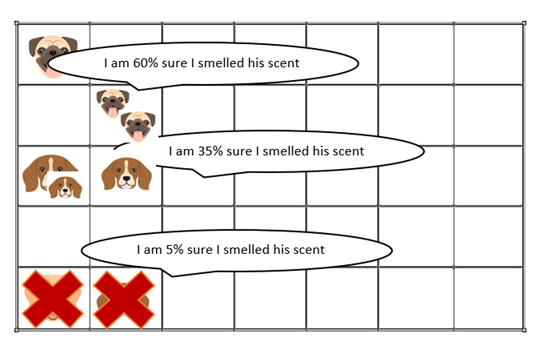
Next, our particles remove follow their mind. Since Particle A is 60% sure it smelled Thanos, we introduce a new dog in its area. Since Particle C in the bottom grid only 5% sure it smelled Thanos, we discard it and let it go back home.
Time = 70 minutes
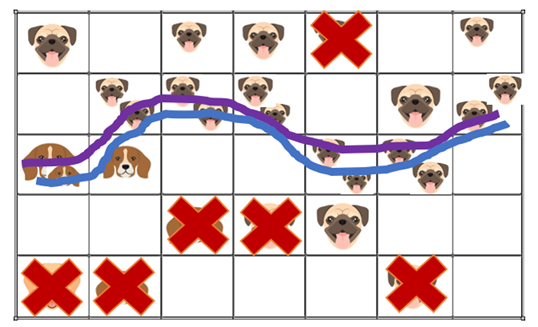
As we see, at time 70 we successfully trace Thanos, and we save the world!
Particle filter with resampling
Due to the limitation of particle filter without sampling, we introduce the resampling scheme in the process. It is easy to understand as we duplicate particles when they have a high probability of getting the right path (like introducing a new dog in that area). In addition, we discard those particles with less probability to find the true path.

This is the intuitive idea behind particle filter! Now you could understand the whole process of particle filter!
For more reading:
https://www.stats.ox.ac.uk/~doucet/doucet_johansen_tutorialPF2011.pdf This is a really good review paper!
http://wwwf.imperial.ac.uk/~nkantas/notes4ltcc.pdf This is a really good tutorial! And the references are very famous papers!
This is a really good cartoon to show the whole process: