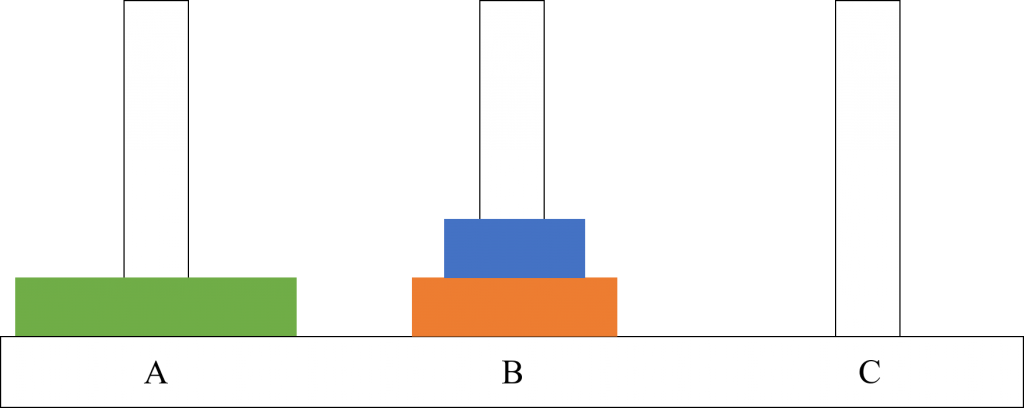
In the puzzle known as Tower of Hanoi (named after the style of buddhist temples in Vietnam, I assume) , you have three rods or pegs and a number of disks of different diameters. The puzzle begins with a set up like the one shown below (for three disks) where all of the disks are placed on one of the rods (rod A) with the largest at the bottom and the smallest at the top. The aim of the puzzle is to move all of these disks from rod A to rod C whilst obeying the following rules:
- Only one disk can be moved at a time
- Only the disk at the top of a stack can be moved
- A disk cannot be placed on top of another disk with smaller diameter

It’s a relatively simple task, with a little trial and error, to solve this puzzle for the three-disk problem shown here but what if there are more disks? Is there some kind of rule we can come up with to be able to solve this no matter the number of disks, \( N [\latex], present? The answer is yes, kind of … In that we can find these rules by leveraging a programming/problem solving concept known as recursion but as I’ll explain later there is something else that limits our ability to solve the problem for large numbers of disks.
The philosophy behind solving problems using recursion is that we break a large problem down into sub-problems which can be solved using the same procedure in a simpler way. The solutions of the subproblems are then collected together to give the solution to the larger problem.
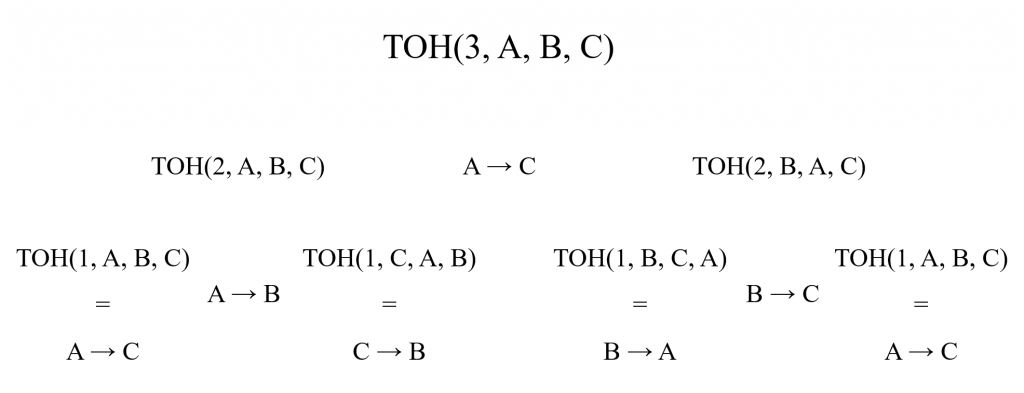
For the tower of Hanoi problem, the important thing to realise is that because of how the puzzle works, at some stage we will have the situation shown below where \(\) (N-1) \) disks are on rod B and we have to move the largest disk from A to C and then all of the remaining disks from B to C. This means that we can break the problem down into the subproblems of moving \( (N-1) \) disks from A to B, moving A to C (which is trivial) and then moving \( (N-1) \) from B to C.
If we were going to write this like a function (called TOH) in a programming language where we would take in a series of arguments and then produce an output which is the solution to the TOH problem, we would get something that looks like this:

The function TOH takes four arguments; the first is the number of disks being moved , \( N \), and the next three arguments indicate the rod being moved from, the intermediate rod and the rod being moved to respectively. In this case, the first function wants to move \( N \) disks from rod A to rod C via rod B. As I mentioned earlier, this can be decomposed into the problem of moving the \( (N-1) \) smaller disks from A to B then moving the largest disk from A to C and then moving the \( (N-1) \) smaller disks from B to C. Notice how this is achieved in this function by executing TOH within TOH with \( (N-1) \) disks being moved from A to B via C then moving A to C and then executing TOH again with \( (N-1) \) disks being moved from B to C via A. These TOH functions with \( (N-1) \) disks as arguments will themselves call TOH functions with \( (N-2) \) disks and so on until TOH is called with \( 0 \) disks as an argument and the function STOPS. This repeated calling of a function within itself is a feature that is common to any kind of recursive method.
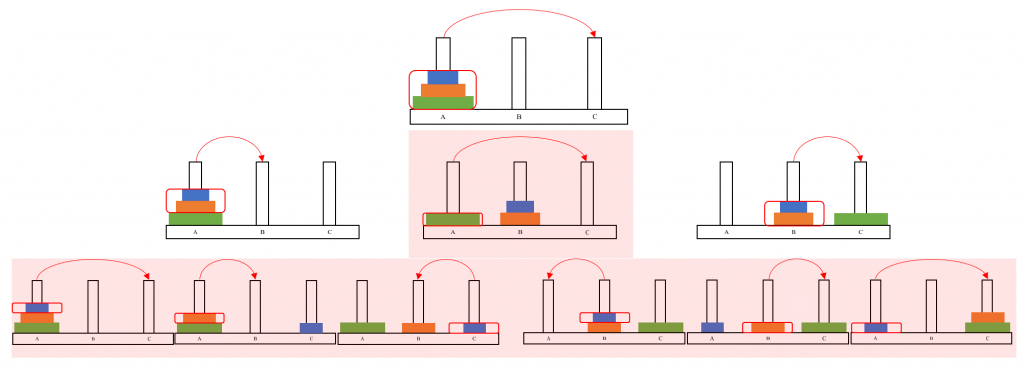
In my opinion, the best way to visualise this recursion is by trying an example. To this end, I have included 2 tree diagrams (Click these diagrams to enlarge them). The first shows which disks are being moved by each TOH function. Notice that the steps highlighted in red are a step by step solution to the puzzle. The second diagram shows the functions to which these steps correspond. Notice that the first function calls the second row of functions that calls the third row. I haven’t included the final row of function calls because these have an \( N = 0 \) argument and therefore stop without making an action.
So, we now how a set of rules that we can employ to solve the tower of Hanoi problem for any number of disks, right? In theory, yes. In practice, no. The reason behind this can be discovered by looking at the number of steps in the solution as \( N \) gets larger. For our example with \( N = 3 \) disks given here, the number of steps to solve the puzzle is 7. It turns out that the number of steps taken to solve the puzzle as a function of \( N \) is \( 2^{N} – 1 \). This is a big problem as you may realise having read my previous blog on the P vs NP problem . A scaling with \( N \) like this means that for \( N = 64 \), which is a fairly modest number the solution has so many steps that even at the rate of one disk moved per second, it would take 42 times the age of the universe to solve the puzzle. Even worse, even if an omnipotent being gave us the solution it would still take this long just to check he wasn’t lying to us. Ouch! Although maybe it’s not such as bad thing. There is a legend about some Indian Brahmin priests that are trying to solve the puzzle with 64 golden disks and should they solve it, the end of the world will come. It’s comforting to know that your plans won’t be interrupted by the world ending, at least for the next 585 billion years.
Relevant Links
Youtube video that covers this topic with some nice animations!


I like the helpful info you provide in your articles. I will bookmark your weblog and check again here frequently. Im quite certain I’ll learn many new stuff right here! Best of luck for the next!