In today’s blog post I want to give a very brief overview of a problem that is so important it features in the Clay Mathematical Institute’s “Millennium Problems“, a list of problems that were considered the most important and challenging unsolved problems in the field of mathematics at the turn of the millennium.
The problem I am going to touch upon today is the enticingly named the “P vs NP problem” (don’t worry the meaning of P and NP will be explained soon). This problem is probably the easiest for a non-mathematician to grasp and even solve if you happen to be minesweeper prodigy (more on this later). It also has great relevance to the field of operational research, so it was a natural choice for a blog post.
Note: Saying that this problem has great relevance to operational research is putting things a bit lightly … more on this later in the post.
The meaning behind P and NP
The crux of this problem is one of computational efficiency. It has stemmed from the desire of researchers to know how efficiently certain problems can be solved by supplying a computer with an algorithm (a set of instructions that will solve the problem for every possible input to that problem). An extremely simple example of an algorithm, and one that most of us are probably familiar with, is shown in the gif below. That’s right, the long multiplication technique that we all learned at school consists of a set of instructions for multiplying two n digit numbers that we could easily program into a computer to let it do the hard work for us. Taking a moment to think about how many steps we would expect this algorithm would take for two relatively small numbers can be quite illuminating. Essentially, we multiply each digit in one of the numbers by all the digits in the other. So for two five digit numbers we would end up multiplying 25 or \( 5^{2} \) digits together in 25 steps. There would also be some additional steps for carrying numbers and addition but the bulk of the steps involve these individual multiplications. In general we say that this algorithm is of order (of order just means that we look at the steps that contribute most) \( n^{2} \), where \( n \) is the number of digits in the numbers being multiplied.
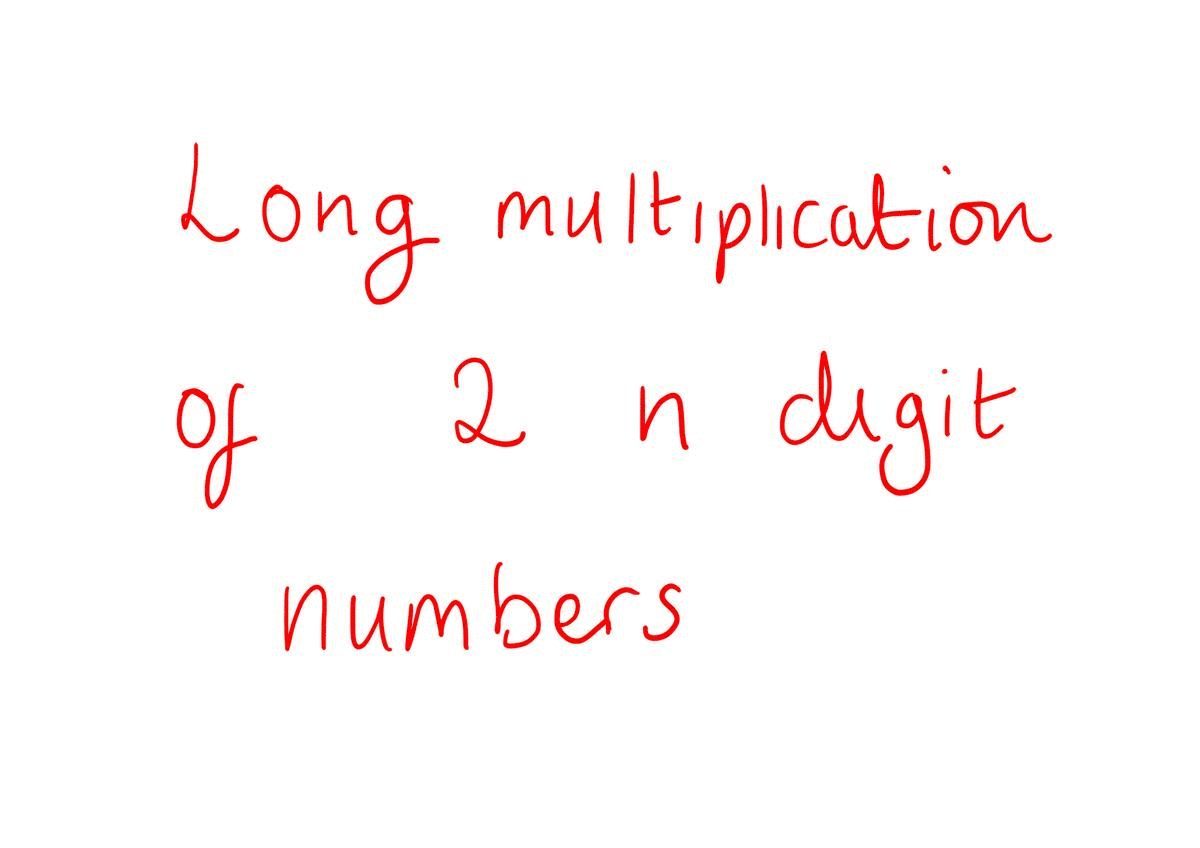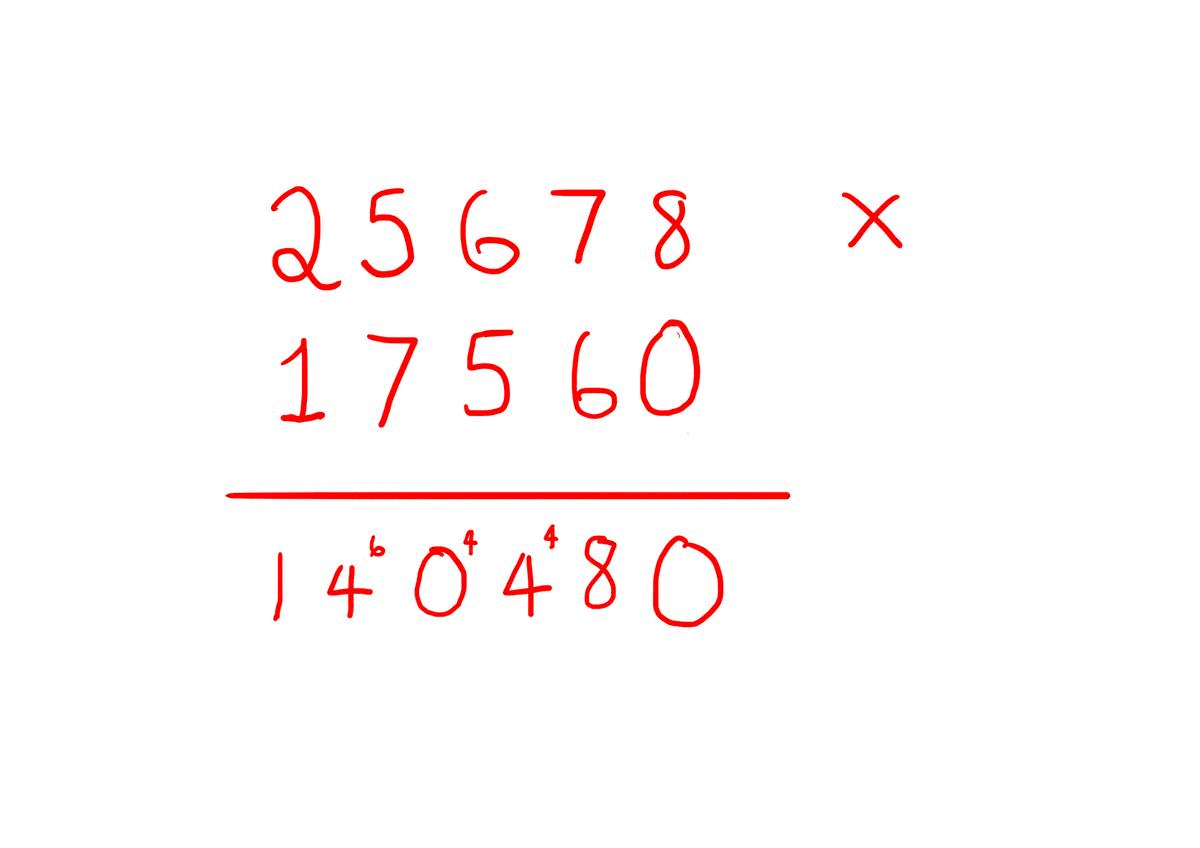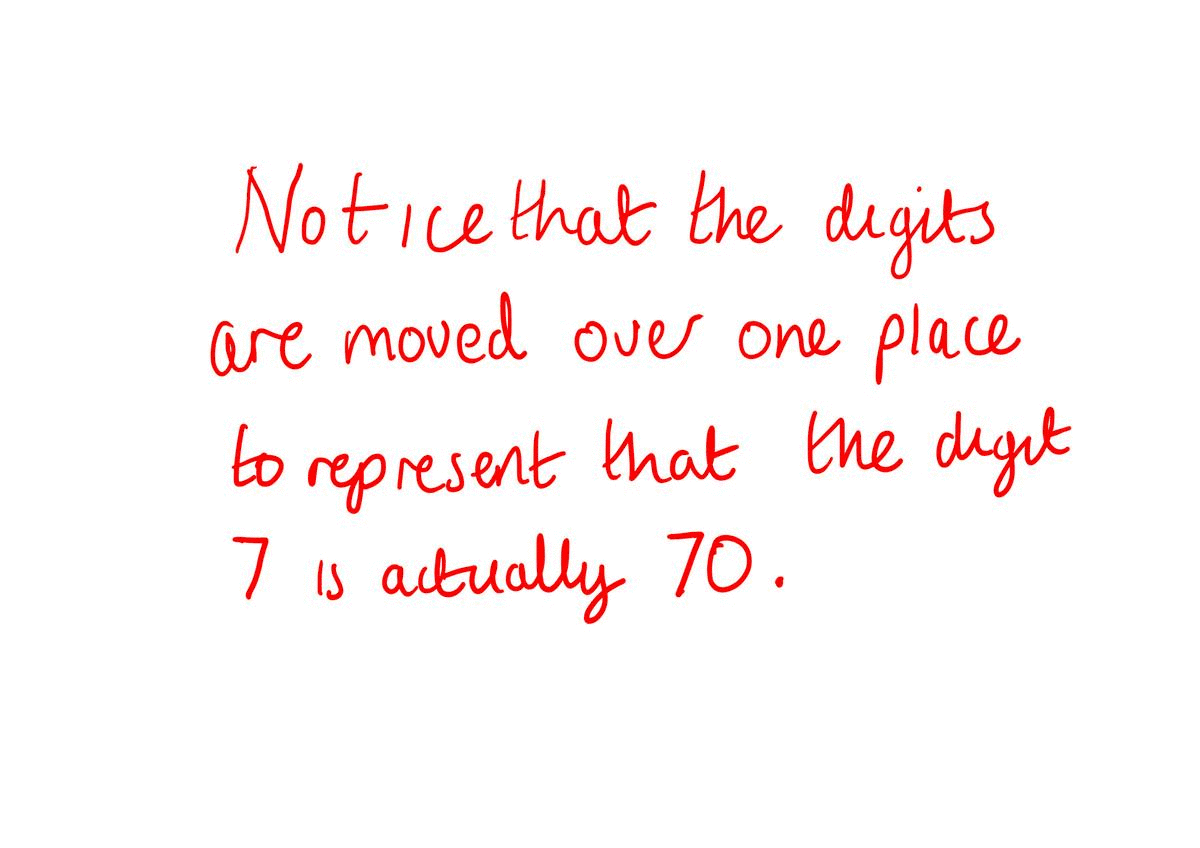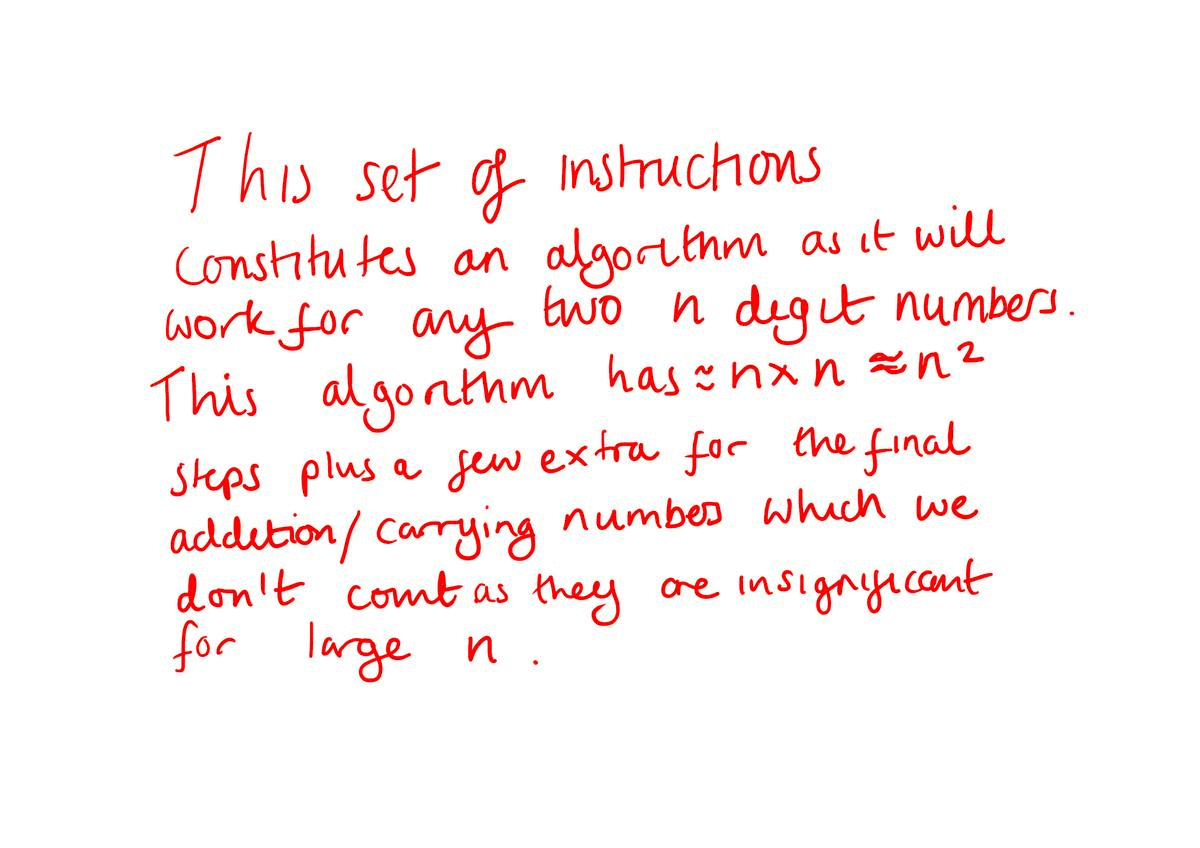
Before defining P and NP, it is important to note that they are defined with respect to decision problems. A decision problem is just a problem in which the solution is a yes or no answer (i.e. does a solution exist?: Yes/No). This isn’t really a limitation because most problems can be configured into decision problems with a bit of thought.
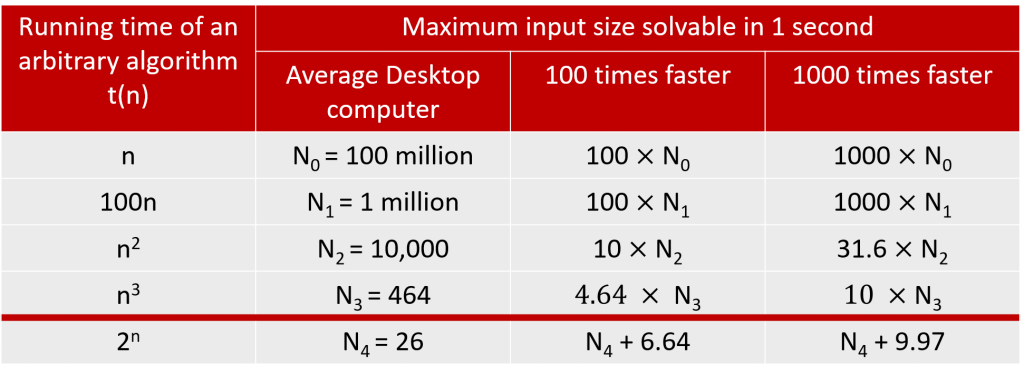
A decision problem is said to belong to the set of problems, P, if it has an algorithm associated with it that takes polynomial time. This means that if you have an input of size \( n \), the worst case running time of the algorithm is of order \( n^{k} \) , where \( k \) is some constant. The multiplication algorithm given above is an example of a polynomial time algorithm that falls into class P. A look at the table below shows why this is an important consideration when trying to create an algorithm. As you can see, we have a range of different polynomial running times, expressed in terms of the input size \( n \), along with what kind of problem sizes we would expect to be able to solve on an average desktop computer and computers 100 and 1000 times faster than it. The main takeaway here is that a polynomial time algorithm, even when \( k \) is quite large (in practice, most algorithms in P have \( k ≤ 4 \)), has the scope to be applied to problems with large n and that n will increase appreciably with an increase in computing power. Note too that increases in computing power of these sizes is very realistic, especially if an algorithm can be designed to run on many computers at once. The second takeaway is in the final row which shows a common running time for an algorithm not in P. You can see why algorithms that do not belong to P are generally considered unusable for large problem instances. Using 1000 times the computing power results in only being able to compute an input size that has approximately 10 additional inputs. This is a shocking result!
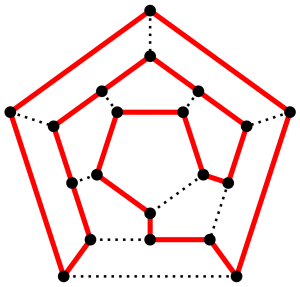
So, what does NP mean? NP stands for Non-deterministic Polynomial time and is a set of problems that do not have a algorithm that can find a solution in polynomial time. However, if you have a solution, there are algorithms that can check if that solution is correct in polynomial time. An example of a problem that is in the set NP is shown below. It is the problem of trying to find out whether a Hamiltonian cycle exists for a given connected graph of vertices. A Hamiltonian cycle is the name given to a path taken around the graph that visits every vertex once before returning to the start. It is shown in red on the graph below. It turns out that there isn’t an algorithm that we know of that works out whether a given graph has a Hamiltonian cycle that takes polynomial time. On the other hand, if we are given a graph with a Hamiltonian cycle, it is a fairly trivial matter of checking if it is a true Hamiltonian cycle and we have a polynomial time algorithm to do so. A quick note here that all problems in the set P belong to the set NP as solving a problem in polynomial time means that by extension we can check it in polynomial time.
There is a subset of problems that belong to the set NP that have a property known as NP-completeness. A problem is said to be NP-complete if all of the other problems in NP can be transformed into it in polynomial time. I won’t go into great detail about the concept of transforming a problem here but it essentially involves adding extra features to a problem so that by solving it you solve a different problem. Transforming in polynomial time just means that any steps involved in the transformation take polynomial time. NP-completeness is a compelling thing because if we could discover a polynomial time algorithm for an NP-complete problem them we would have a polynomial time algorithm we could apply to every problem in NP.
It turns out that a lot of important problems in many important fields belong to the set NP, an example being the travelling salesman problem in operational research. The “P vs NP problem” is the problem that we don’t know whether the fact that we do not have polynomial time algorithms for NP problems is due to a lack of human inventiveness or due to the fact that there will never be a polynomial time algorithm for NP problems. Most researchers currently believe that P ≠ NP but it would be necessary to produce a rigorous mathematical proof of this to put the P vs NP problem to rest. This is not a straightforward task at all, how do you go about showing that there will never be a method that can be used to solve any NP-complete problem in polynomial time. In fact, there is research that shows that current methods of obtaining mathematical proofs are not powerful enough to prove P ≠ NP.
On the other hand, there is the enticing possibility that P = NP. In theory, this is a much easier thing to prove because it would require the creation of a polynomial time algorithm for one of the many thousands of NP-complete problems. This is where minesweeper comes in, it turns out that minesweeper has been proven to be an NP-complete problem and therefore if you were to able to come up with an algorithm that solves a minesweeper grid of size \( n \) in time \( n^k \), you will have proved that P = NP. The hilarious conclusion to this would be that it would turn out that the best way to solve serious operational research problems such as integer programming and travelling salesman would be to convert them into a game of minesweeper.
I think that sums up the consequences of a proof that P = NP. It would be completely insane and world altering. Suddenly we would be able to solve incredibly complicated problems that we could have only dreamed of solving before such as protein folding and cryptography and that’s just thinking of immediate and somewhat narrow minded consequences. Not all problems belong to just the sets P and NP however, there are other problems such as deciding if a chess move is the best possible move that take non-polynomial time to even evaluate whether a given solution is the best move (you essentially have to play every possible continuation to the chess game after that move). A proof of P = NP would not mean that we could easily solve every possible problem.
A proof that P ≠ NP would certainly be a bit more mundane but it would still put the problem to rest and allow researchers to completely focus on alternative heuristic solutions to NP problems which attempt to give good solutions in most but not all cases of the problem. In fact, the fruitlessness of the search for polynomial time algorithms for NP problems means that this shift in research focus has already begun to happen but there are still many who have not given up hope of finding that elusive algorithm just yet …
Relevant Links
Statement of the P vs NP problem
Proposed (and debunked) proofs
I have read so many posts about the blogger lovers however this post is really a good piece of writing, keep it up
whoah this blog is wonderful i really like reading your articles. Keep up the great paintings! You realize, a lot of people are hunting round for this info, you could help them greatly.
whoah this blog is wonderful i really like reading your articles. Keep up the great paintings! You realize, a lot of people are hunting round for this info, you could help them greatly.
Can I put some of this on my page if I include a link to this website?
Sure, as long as you credit it its fine 🙂
There are Wormsholes in Physics to go faster and further so , why not in Mathematics ? P = NP !! Other arguments : It`s positive and we put a bar less !
useful blog currently looking for a research project as to why we haven’t solved this problem if you got any ideas for sections i could add to this it would be appreciated
A good place to look for additional resources is: https://www.claymath.org/millennium/p-vs-np/. There are some video lectures linked here that may help give some additional insight into the problem.