A while ago, when I was in the “MOOCs are great!” phase of my life, I took an online course on negotiation. I never finished the practical part of it, but I remember the theory being surprisingly mathematical. It centred around constructing theoretically sound mathematical concepts of “fairness” and then applying them to a variety of different scenarios to construct an “optimally fair to all parties” solution – accompanied, of course, by an explanation of the various ways people attempt to obscure this to skew the negotiation situation in their favour.
A simple example of mathematical fairness is known as the “Principle of the Divided Cloth”, and it goes all the way back to the Talmud. If there is a roll of cloth that person A claims to own all of and person B claims to own half of, how should it be divided? Well, assuming the claims are both reasonable, one would be tempted to split the cloth in proportion to the amount that was claimed by each side, in a 2:1 ratio. However, the Principle of the Divided Cloth instead proposes a 3:1 split, following the logic that only half of the cloth is in dispute – nobody is saying that A doesn’t own the first half – so the disputed part should be split equally.
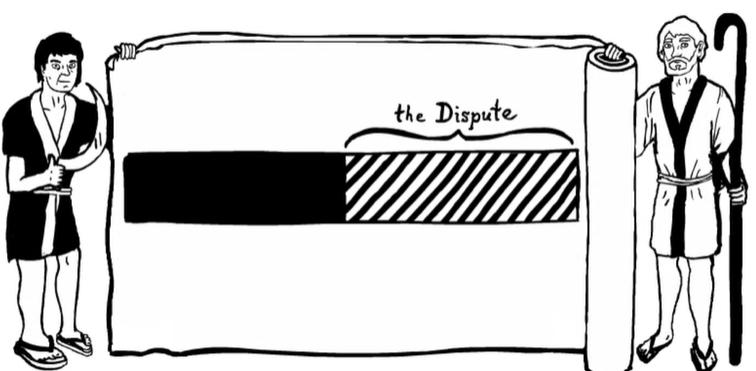
This principle can be applied to a wide variety of problems where two (or more) parties can come together to create something more valuable than they could working apart, and must decide how to divide that extra value.
Fairness in Optimisation
In an optimisation problem, you’re trying to locate the “best” solution. “Best” how and for whom, you ask? Good question. The usual answer is “best for whomever is paying me and however they define ‘best'”. However, in applying optimisation methods to complex problems when multiple parties have stakes in the outcome, you can find yourself unwillingly appointed to the position of arbitrator.
The example we’ve looked at in STOR-i relates to the OR-MASTER project about scheduling flight capacity on airport runways. The airport itself would like as much capacity as possible to be used (making it extra money), without going over capacity and causing delays as planes are held up for lack of runways. Each airline wants to be able to schedule its flights to take off and land whenever it wants, which may include during “peak periods” when the runways are too busy to accommodate everyone’s requests. The airlines as a collective want a solution they understand the mechanics of that means they don’t have to play convoluted guessing games with to get the flight slots they want.
There are two conflicts at play here:
- Each airline is competing with every other airline that uses that airport’s runways. We need to ensure the optimisation result is “fair” to every airline.
- The airlines as a collective are in competition with the airport when it comes to what they want from this optimisation. We need to balance the airlines’ need for “fairness” against the airport’s need for “maximum capacity in use”.
The first problem is solved by constructing a mathematical definition of “fairness”, which in this case is approximately “You get out of life what you put into it”. Airlines requesting slots in peak periods are likely to have their slot requests moved around. The more peak slots they request, the more movement they will have to put up with. We can construct a “coefficient of fairness” for each airline that quantified how fairly it has been treated by our optimiser, and then try to keep everyone’s fairness coefficient similar.
The second problem is harder to put in maths, because airlines and airports are not the same thing, so it’s hard to say what “equal treatment” means. Also, there’s nothing to say we should be treating them equally – that decision is better made by experts in the field of aviation than by us.
We solve this by constructing what’s called a “Pareto Frontier”, or a range of solutions that balance one objective (fairness) against another (capacity). Each point on the frontier is “optimal” in the sense that for the same capacity there is no fairer solution and for the same fairness there is no solution with more capacity.
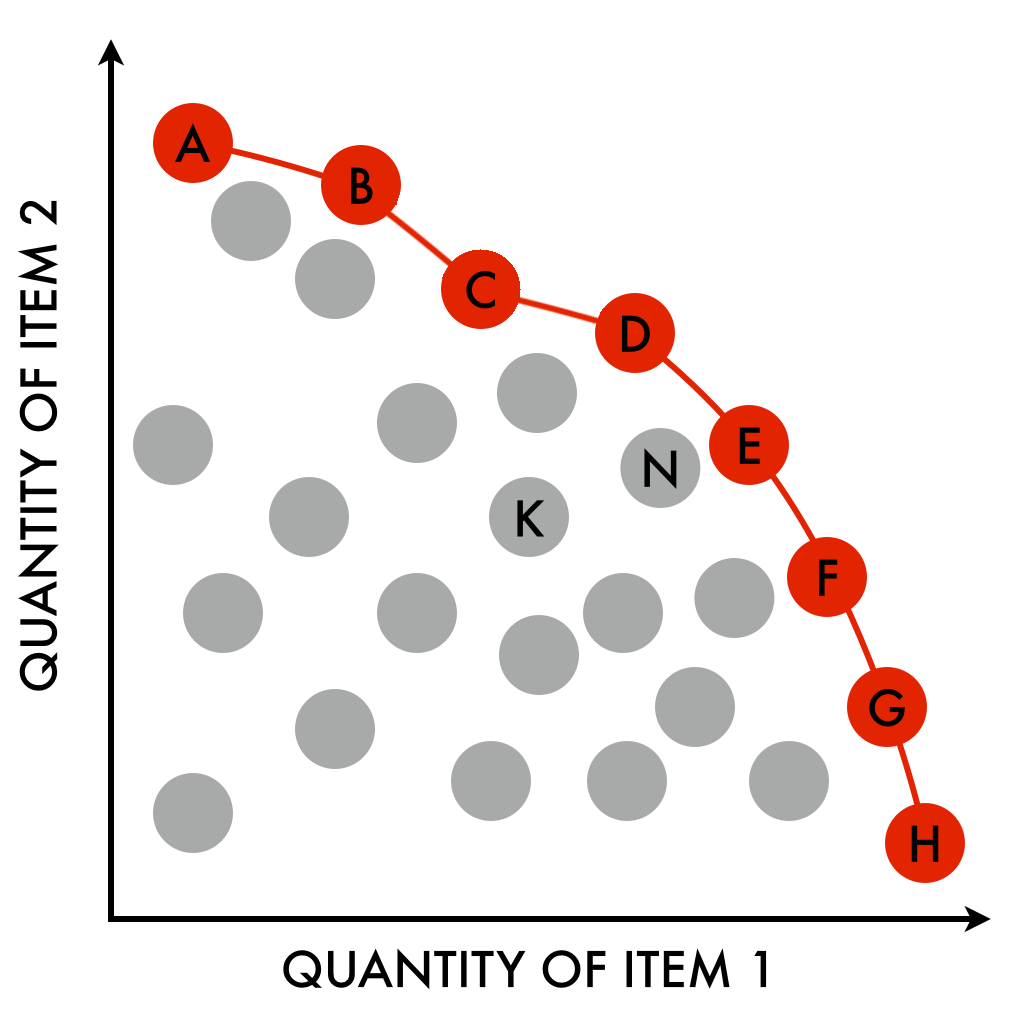
Then, we can give this solution set over to the representatives of the airlines and airports to negotiate over, washing our hands of the problem.
It turns out in practice we can get a lot of what’s called “easy wins” – by sacrificing a small amount from “optimal capacity”, we can make the solution a lot more fair. This is visible in the diagram above as the slope of the frontier being flatter near the top. So by implementing any fairness metric at all in our optimisation, we can keep multiple parties happier.